Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bắt chước theo giang hồ đại ca . 5 phút nữa sẽ ra đáp án

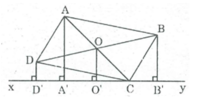
Gọi O là giao điểm của hai đường chéo AC và BD.
Kẻ OO' ⊥ xy
Ta có: BB' ⊥ xy (gt)
DD' ⊥ xy (gt)
Suy ra: BB // OO' // DD'
Tứ giác BB'D'D là hình thang .
OB = OD (t/chất hình bình hành)
Nên O'B' = O'D'
Do đó OO' là đường trung bình của hình thang BB'D'D
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung hình hình thang) (1)
AA' ⊥ xy (gt)
OO' ⊥ xy (theo cách vẽ)
Suy ra: AA' // OO'
Trong ∆ ACA' tacó: OA = OC (tính chất hình bình hành)
OO' // AA' nên OO' là đường trung bình của ∆ ACA'
⇒ OO' = 1/2 AA' (tính chất đường trung bình của tam giác)
⇒ AA' = 2OO' (2)
Tử (1) và (2) suy ra: AA' = BB' + DD'

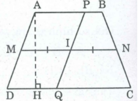
Giả sử hình thang ABCD có AB // CD, đường trung bình là MN. Gọi I là trung điểm của MN, đường thẳng bất kỳ đi qua I cắt AB tại P và CD tại Q.
Ta có hai hình thang APQD và BPQC có cùng đường cao.
MI là đường trung bình của hình thang APQD.
Suy ra: MI = 1/2 (AP + QD)
IN là đường trung bình của hình thang BPQC.
Suy ra: IN = 1/2 (BP + QC)
S A P Q D = 1/2 (AP + QD).AH = MI.AH (1)
S B P Q C = 1/2 (BP + QC).AH = IN.AH (2).
IM = IN (gt) (3)
Từ (1), (2) và (3) suy ra: S A P Q D = S B P Q C , các giá trị này không phụ thuộc vào vị trí của P và Q.
