Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{KA}=-\overrightarrow{AK}=-\frac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=-\frac{1}{2}\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\right)\)
\(=-\frac{1}{4}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}\)
\(\overrightarrow{KD}=\overrightarrow{AD}-\overrightarrow{AK}=\overrightarrow{AD}+\overrightarrow{KA}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\frac{1}{4}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}\)
\(=\frac{1}{4}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\)

HD: \(\overrightarrow{BC}=\frac{-2}{3}\overrightarrow{AM}+\frac{4}{3}\overrightarrow{AN};\overrightarrow{CD}=\frac{-4}{3}\overrightarrow{AM}+\frac{2}{3}\overrightarrow{AN}\)

Câu 1:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
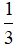
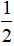
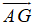
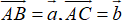
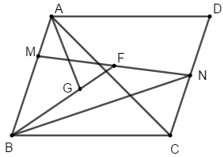

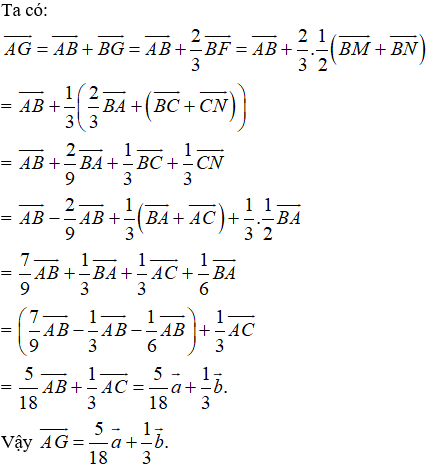
Lời giải:
a.
$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$ (tính chất hình bình hành)
b.
$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AC}=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{AD})$
c.
$\overrightarrow{AN}=\overrightarrow{AC}+\overrightarrow{CN}=\overrightarrow{AC}+\frac{1}{2}\overrightarrow{BA}$
$=\overrightarrow{AB}+\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$
$=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}$