Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1:
Gọi O là giao điểm của AC và BD.

Ta có:
\(\begin{array}{l}\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {BG} = \overrightarrow a + \overrightarrow {BG} ;\\\overrightarrow {CG} = \overrightarrow {CB} + \overrightarrow {BG} = \overrightarrow {DA} + \overrightarrow {BG} = - \overrightarrow b + \overrightarrow {BG} ;\end{array}\)(*)
Lại có: \(\overrightarrow {BD} =\overrightarrow {BA} + \overrightarrow {AD} = - \overrightarrow a + \overrightarrow b \).
\(\overrightarrow {BG} ,\overrightarrow {BD} \) cùng phương và \(\left| {\overrightarrow {BG} } \right| = \frac{2}{3}BO = \frac{1}{3}\left| {\overrightarrow {BD} } \right|\)
\( \Rightarrow \overrightarrow {BG} = \frac{1}{3}\overrightarrow {BD} = \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right)\)
Do đó (*) \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AG} = \overrightarrow a + \overrightarrow {BG} = \overrightarrow a + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\\\overrightarrow {CG} = -\overrightarrow b + \overrightarrow {BG} = -\overrightarrow b + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b ;\end{array} \right.\)
Vậy \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .\)
Cách 2:
Gọi AE, CF là các trung tuyến trong tam giác ABC.
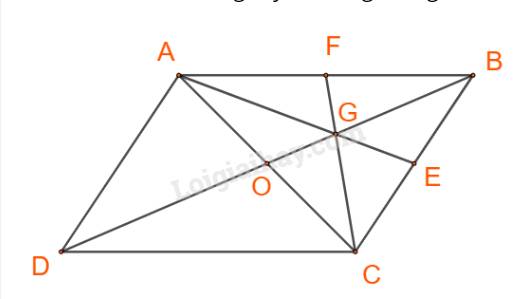
Ta có:
\(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AE} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\overrightarrow {AB} + \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)} \right] \\= \frac{1}{3}\left( {2\overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
\(\overrightarrow {CG} = \frac{2}{3}\overrightarrow {CF} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\left( {\overrightarrow {CB} + \overrightarrow {CD} } \right) + \overrightarrow {CB} } \right] = \frac{1}{3}\left( {2\overrightarrow {CB} + \overrightarrow {CD} } \right) = \frac{1}{3}\left( { - 2\overrightarrow {AD} - \overrightarrow {AB} } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b \)
Vậy \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .\)

a) Ta có:
\(\overrightarrow {DM} = \overrightarrow {DA} + \overrightarrow {AM} = - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} \) (do M là trung điểm của AB)
\(\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {BN} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \) (do N là trung điểm của BC)
b)
\(\begin{array}{l}\overrightarrow {DM} .\overrightarrow {AN} = \left( { - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} } \right).\left( {\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} } \right)\\ = - \overrightarrow {AD} .\overrightarrow {AB} - \frac{1}{2}{\overrightarrow {AD} ^2} + \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{1}{4}\overrightarrow {AB} .\overrightarrow {AD} \end{array}\)
Mà \(\overrightarrow {AB} .\overrightarrow {AD} = \overrightarrow {AD} .\overrightarrow {AB} = 0\) (do \(AB \bot AD\)), \({\overrightarrow {AB} ^2} = A{B^2} = {a^2};{\overrightarrow {AD} ^2} = A{D^2} = {a^2}\)
\( \Rightarrow \overrightarrow {DM} .\overrightarrow {AN} = - 0 - \frac{1}{2}{a^2} + \frac{1}{2}{a^2} + \frac{1}{4}.0 = 0\)
Vậy \(DM \bot AN\) hay góc giữa hai đường thẳng DM và AN bằng \({90^ \circ }\).

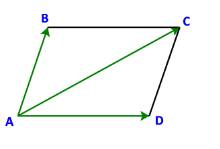
a) Ta có: \(\left\{ \begin{array}{l}AD//BC\\AD = BC\end{array} \right.\) (do tứ giác ABCD là hình bình hành)
\( \Rightarrow \overrightarrow {AD} = \overrightarrow {BC} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)

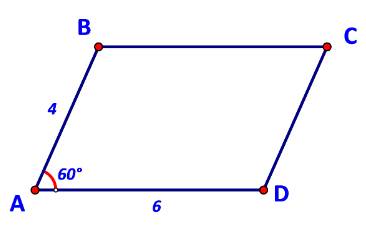
a) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)
c) Áp dụng định lí cosin cho tam giác ABD ta có:
\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)

Bài 1:
Gọi K là trung điểm của BC
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔCAB có
O,K lần lượt là trung điểm của CA,CB
=>OK là đường trung bình
=>OK//AB và \(OK=\dfrac{AB}{2}\)
=>\(\overrightarrow{OK}=\dfrac{\overrightarrow{AB}}{2}\)
=>\(\overrightarrow{AB}=2\cdot\overrightarrow{OK}\)
Xét ΔOBC có OK là đường trung tuyến
nên \(\overrightarrow{OB}+\overrightarrow{OC}=2\cdot\overrightarrow{OK}\)
=>\(\overrightarrow{AB}=\overrightarrow{OB}+\overrightarrow{OC}\)
=>M trùng với B
Bài 2:
Xét ΔABC có
M,P lần lượt là trung điểm của AB,AC
=>MP là đường trung bình của ΔABC
=>MP//BC và MP=BC/2
=>MP=CN
mà MP//NC
nên MPCN là hình bình hành
=>\(\overrightarrow{MP}=\overrightarrow{NC}\)
=>\(\overrightarrow{MP}=-\overrightarrow{CN}\)
=>\(\overrightarrow{MP}+\overrightarrow{CN}=\overrightarrow{0}\)
mà \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\)
nên K trùng với P

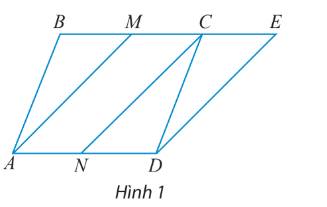
a) Ta có: \(\overrightarrow {CE} = \overrightarrow {AN} \Rightarrow CE//AN\) và \(CE = AN = ND = BM = MC\)
Suy ra \(\overrightarrow {MC} = \overrightarrow {CE} \)
+) \(\overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CE} = \overrightarrow {NE} \)
+) ABCD là hình bình hành nên \(\overrightarrow {CD} = \overrightarrow {BA} \)
\(\overrightarrow {AM} + \overrightarrow {CD} = \overrightarrow {AM} + \overrightarrow {BA} = \overrightarrow {BM} \)
+) Ta có \(\overrightarrow {MC} = \overrightarrow {AN} \Rightarrow AMCN\) là hình bình hành nên \(\overrightarrow {NC} = \overrightarrow {AM} \)
\(\overrightarrow {AD} + \overrightarrow {NC} = \overrightarrow {AD} + \overrightarrow {AM} = \overrightarrow {AE} \) (vì AMED là hình bình hành)
b) Ta có:
+) \(\overrightarrow {NC} - \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CM} = \overrightarrow {NM} \)
+) \(\overrightarrow {AC} - \overrightarrow {BC} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \)
+) \(\overrightarrow {AB} - \overrightarrow {ME} = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB} \)
c) Ta có:
\(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AM} + \overrightarrow {MC} = \overrightarrow {AC} \)
Áp dụng quy tắc hình bình hành vào hình bình hành ABCD ta có
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Từ đó suy ra \(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD} \) (đpcm)
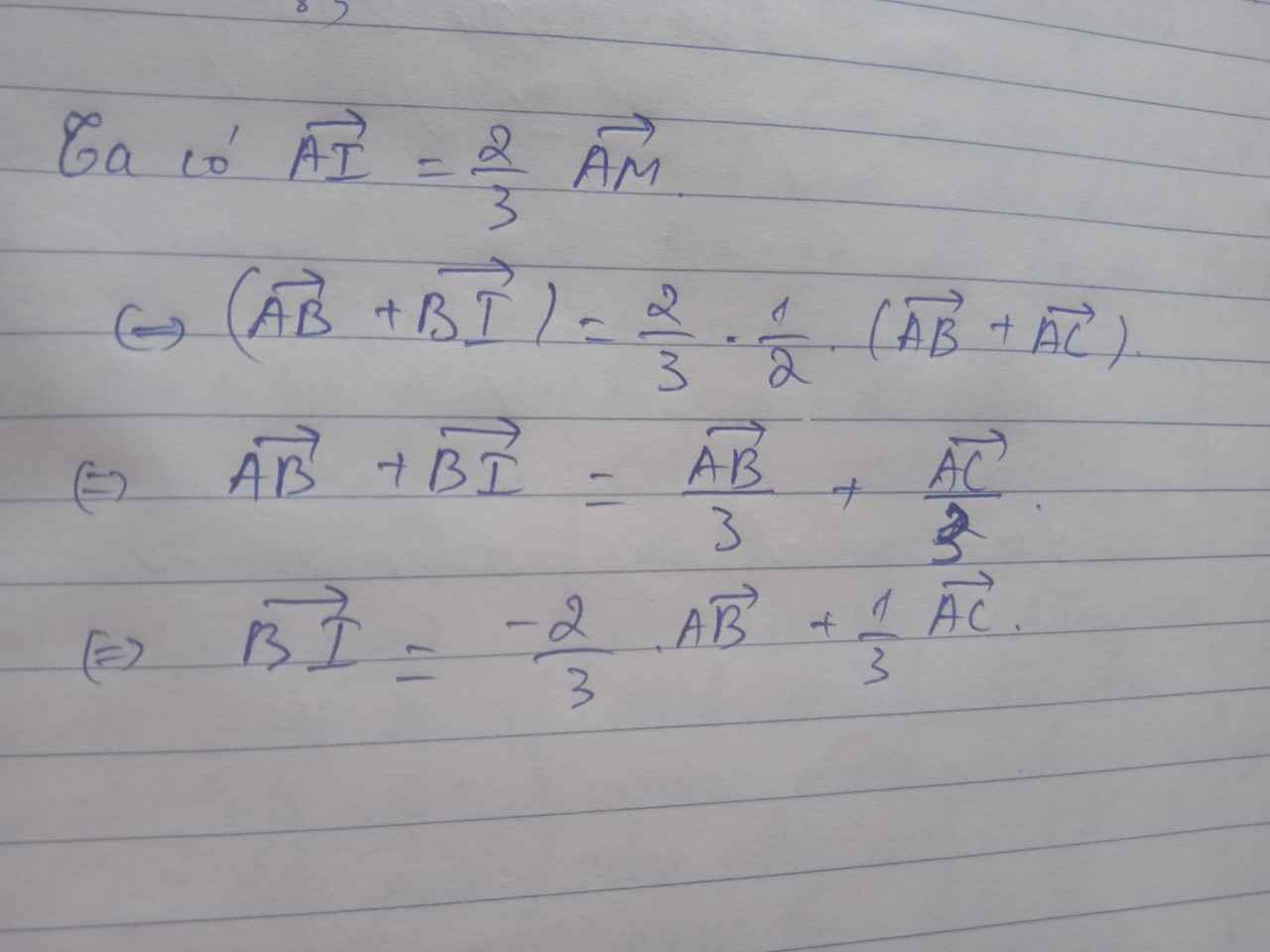
Từ M kẻ đường thẳng song song với AB, cắt AD tại E.
Khi đó tứ giác ABME là hình bình hành.
Do đó: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AE} \).
Dễ thấy: \(AE = BM = \frac{1}{2}BC = \frac{1}{2}AD\)
\( \Rightarrow \overrightarrow {AE} = \frac{1}{2}\overrightarrow {AD} \)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \)
Vậy \(\overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \)
Chú ý khi giải
+) Dựng hình hình hành sao cho đường chéo là vecto cần biểu thị, 2 cạnh của nó song song với giá của hai vecto đang biểu thị theo.