Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì EB= \(\frac{AB}{2}\)
DF= \(\frac{DC}{2}\)
Mà AB=CD (hình bình hành)
=> EB= DF
Tứi giác EBFD có
EB // DF; EB=DF nên là hbh
Do đó: ED// BF
Xét \(\Delta CDM\) có: DF=CF ; FN// DM nên NC= NM (1)
Xét \(\Delta ABN\) có: AE=BE ; EM// BN nên MN= AM(2)
Từ (1) và (2) suy ra AM=MN=NC
Chúc bạn học tốt

A B C D E F M N
Xét tam giác ADE và tam giác BCF có AD = BC (ABCD là hình bình hành)
Góc BAD = góc BCD , AE = CF = 1/2AB = 1/2CD
=> tam giác ADE = tam giác BCF (c.g.c)
=> góc AED = góc CFB . Mà AB // CD => góc CFB = góc ABF
=> góc AED = góc ABF mà hai góc này ở vị trí đồng vị
=> DE // BF
Xét tam giác MCD có NF // MD , DF = FC => NF là đường trung bình tam giác MCD
=> MN = NC (1)
Tương tự , ta cũng có ME là đường trung bình của tam giác ANB
=> AM = MN (2)
Từ (1) và (2) suy ra AM = MN = NC (đpcm)

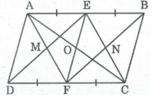
Gọi O là giao điểm của AC và EF
Tứ giác AECF là hình bình hành ⇒ OE = OF
Tứ giác EMFN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Suy ra: MN đi qua trung điểm O của EF.
Vậy AC, EF, MN đồng quy tại O.
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
Suy ra: DE//BF
Xét ΔABN có
E là trung điểm của AB
EM//NB
Do đó: M là trung điểm của AN
hay AM=MN(1)
Xét ΔDCD có
F là trung điểm của CD
FN//MD
DO đó: N là trung điểm của MC
Suy ra: MN=NC(2)
Từ (1) và (2) suy ra AM=MN=NC