Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF

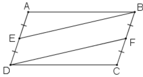
Cách 1:
+ ABCD là hình bình hành ⇒ AB = CD, AD = BC, Â = Ĉ.
+ E là trung điểm của AD ⇒ AE = AD/2
F là trung điểm của BC ⇒ CF = BC/2
Mà AD = BC (cmt) ⇒ AE = CF.
+ Xét ΔAEB và ΔCFD có: AB = CD, Â = Ĉ, AE = CF (cmt)
⇒ ΔAEB = ΔCFD (c.g.c)
⇒ EB = DF.
Cách 2:
ABCD là hình bình hành ⇒ AD//BC và AD = BC.
+ AD // BC ⇒ DE // BF
+ E là trung điểm của AD ⇒ DE = AD/2
F là trung điểm của BC ⇒ BF = BC/2
Mà AD = BC ⇒ DE = BF.
+ Tứ giác BEDF có:
DE // BF và DE = BF
⇒ BEDF là hình bình hành
⇒ BE = DF.
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và .

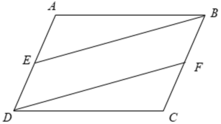
Xét tứ giác BEDF có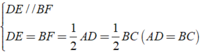
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên
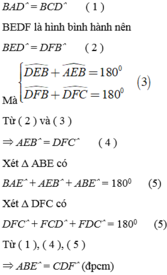

a) Ta chứng minh được BEDF là hình bình hành Þ BE = DF và E B F ^ = C D F ^ .
Cách khác: DAEB = DCFD (c.g.c) suy ra BE = DF và A B E ^ = C D F ^ .

b) Vì BEDF hình bình hành Þ ĐPCM

A B C D E F
Bài này có 2 cách nha bạn
Cách 1:
+ ABCD là hình bình hành => AB = CD, AD = BC, \(\widehat{A}=\widehat{C}\)
+ E là trung điểm của AD \(\Rightarrow AE=\frac{AD}{2}\)
F là trung điểm của BC \(\Rightarrow CF=\frac{BC}{2}\)
Mà AD = BC (cmt) => AE = CF.
+ Xét ΔAEB và ΔCFD có: AB = CD, \(\widehat{A}=\widehat{C}\), AE = CF (cmt)
=> ΔAEB = ΔCFD (c.g.c)
=> EB = DF.
Cách 2:
ABCD là hình bình hành => AD//BC và AD = BC.
+ AD // BC => DE // BF
+ E là trung điểm của AD \(\Rightarrow DE=\frac{AD}{2}\)
F là trung điểm của BC \(\Rightarrow BF=\frac{BC}{2}\)
Mà AD = BC => DE = BF.
+ Tứ giác BEDF có:
DE // BF và DE = BF
=> BEDF là hình bình hành
=> BE = DF

mk sửa lại đề nha: chứng minh rằng BE = DF
ABCD là hình bình hành \(\Rightarrow\)AB = CD; AD = BC; \(\widehat{A}\)= \(\widehat{C}\)
E là trung điểm AD \(\Rightarrow\)EA = \(\frac{AD}{2}\)
F là trung điểm BC \(\Rightarrow\)CF = \(\frac{BC}{2}\)
mà AD = BC nên AE = CF
Xét \(\Delta\)AEB và \(\Delta\)CFD có:
AB = CD (cmt)
\(\widehat{A}\)= \(\widehat{C}\) (cmt)
AE = CF (cmt)
suy ra; \(\Delta\)AEB = \(\Delta\)CFD (c.g.c)
suy ra BE = DF (2 cạnh tương ứng)

mình gợi ý cho bạn là ra ngay nhé ! bạn hãy nhớ kiến thức chứng minh tam giác bằng nhau và dùng sơ đồ tư duy ạ ! bài này chứng minh cặp tam giác EBF và EFD sẽ có EF chung , ED=BF vì E là TĐ AD thì EA=ED ; F là TĐ BC thì FB=FC , mà AD =BC thì 2 cạnh đối của HBH , lại thấy AD//BC ( tính chất của HBH) =>> góc FED=góc BFE (slt)
bài này rất dễ ra nếu bạn nắm chắc kiến thức cơ bản , lí thuyết của bài HBH nhé !
Mình gợi ý như vậy chắc bạn ra rồi ! good luck !
ABCD là hình bình hành => AB = CD ; góc A = góc C ; AD = BC
E là trung điểm AD \(\Rightarrow\)\(AE=\frac{AD}{2}\)
F là trung điểm của BC \(\Rightarrow\)\(FC=\frac{BC}{2}\)
Mà AD = BC
Nên AE = FC
Xét \(\Delta ABE\)và \(\Delta CDF\)
\(\widehat{A}=\widehat{C}\)
\(AE=FC\)( cmt )
\(AB=CD\)( cmt )
\(\Rightarrow\)\(\Delta ABE=\Delta CDF\left(c-g-c\right)\)
\(\Rightarrow\)\(BE=DF\)( đpcm )

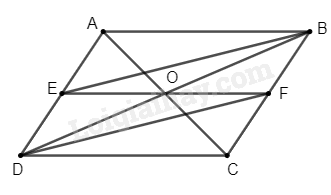
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Mà \(E\), \(F\) là trung điểm của \(AD\), \(BC\) (gt)
Suy ra \(AE = ED = BF = FC\)
Xét tứ giác \(EBFD\) ta có:
\(ED = FB\) (cmt)
\(ED\) // \(BF\) (do \(AD\) // \(BC\))
Suy ra \(EDFB\) là hình bình hành
b) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Mà \(DEBF\) là hình bình hành (gt)
Suy ra \(O\) cũng là trung điểm của \(EF\)
Suy ra \(E\), \(O\), \(F\) thẳng hàng
Bài giải:
Tứ giác BEDF có:
DE // BF ( vì AD // BC)
DE = BF \(\left(DE=\dfrac{1}{2}AD=\dfrac{1}{2}BC=BF\right)\)
Nên BEDF là hình bình hành.
Suy ra BE = DF.
A B D C E F ) ( x x = = = =
Xét \(\Delta ABF\) và \(\Delta CDE\) có :
\(AB=CD\left(gt\right)\)
Góc \(A\) \(=\) Góc \(B\) \((gt)\)
\(AE=CF\left(=\dfrac{1}{2}AD=\dfrac{1}{2}BC\right)\)
Vậy \(\Delta ABE=\Delta CDF\left(c.g.c\right)\)
\(\Rightarrow BE=DF\) (2 cạnh tương ứng)
P/s : Đây là lần đầu em vẽ hình trên máy nên dễ sai sót ạ,với lại em khong thấy kí hiệu góc ở đâu ạ :v Thông cảm cho em