Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Ta có: \(AE=EB=\frac{AB}{2}\)
\(DF=FC=\frac{DC}{2}\)
mà AB=DC
nên AE=EB=DF=FC
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
=>ED//BF
=>EM//FN
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
=>AF//CE
=>EN//FM
Xét tứ giác EMFN có
EM//FN
EN//FM
Do đó: EMFN là hình bình hành
b: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường(1)
EMFN là hình bình hành
=>EF cắt MN tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AC,EF,MN đồng quy
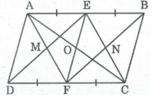
Gọi O là giao điểm của AC và EF
Tứ giác AECF là hình bình hành ⇒ OE = OF
Tứ giác EMFN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Suy ra: MN đi qua trung điểm O của EF.
Vậy AC, EF, MN đồng quy tại O.
a, Ta có: ABCD la hình bình hành
=> AB=CD; AB//CD
Mà E là trung điểm của AB; F là trung điểm của CD.
=>AE= EB= CF= DF (1)
VÌ AB// CD=>EB// DF (2)
Từ(1) và (2) => EBFD là hình bình hành (theo dấu hiệu nhận biết hình bình hành)(đpcm)
b, Xét hbh ABCD ta có:
AC cắt BD tại trung điểm của AC và BD (1)
Xét hình bình hành EBFD có EF cắt BD tại trung điểm của EF và BD (2)
Từ (1) và (2) => Ba đường thẳng AC, BD, EF đồng quy
a: BE=AB/2
DF=DC/2
mà AB=DC
nên BE=DF
Xét tứ giác BEDF có
BE//DF
BE=DF
=>BEDF là hình bình hành
=>DE=BF
b: BEDF là hbh
=>BD cắt EF tại trung điểm của mỗi đường(1)
ABCD là hbh
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra AC,BD,EF đồng quy