Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trug điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: Để AMCK là hình vuông thì AM=CM
=>AM=BC/2
=>ΔABC vuông tại A

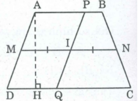
Giả sử hình thang ABCD có AB // CD, đường trung bình là MN. Gọi I là trung điểm của MN, đường thẳng bất kỳ đi qua I cắt AB tại P và CD tại Q.
Ta có hai hình thang APQD và BPQC có cùng đường cao.
MI là đường trung bình của hình thang APQD.
Suy ra: MI = 1/2 (AP + QD)
IN là đường trung bình của hình thang BPQC.
Suy ra: IN = 1/2 (BP + QC)
S A P Q D = 1/2 (AP + QD).AH = MI.AH (1)
S B P Q C = 1/2 (BP + QC).AH = IN.AH (2).
IM = IN (gt) (3)
Từ (1), (2) và (3) suy ra: S A P Q D = S B P Q C , các giá trị này không phụ thuộc vào vị trí của P và Q.


Vì \(\Delta ODE=\Delta OBF\left(g.c.g\right)\)
nên \(OE=OF\)
Do O là trung điểm của EF nên E và F đối xứng với nhau qua O
