Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

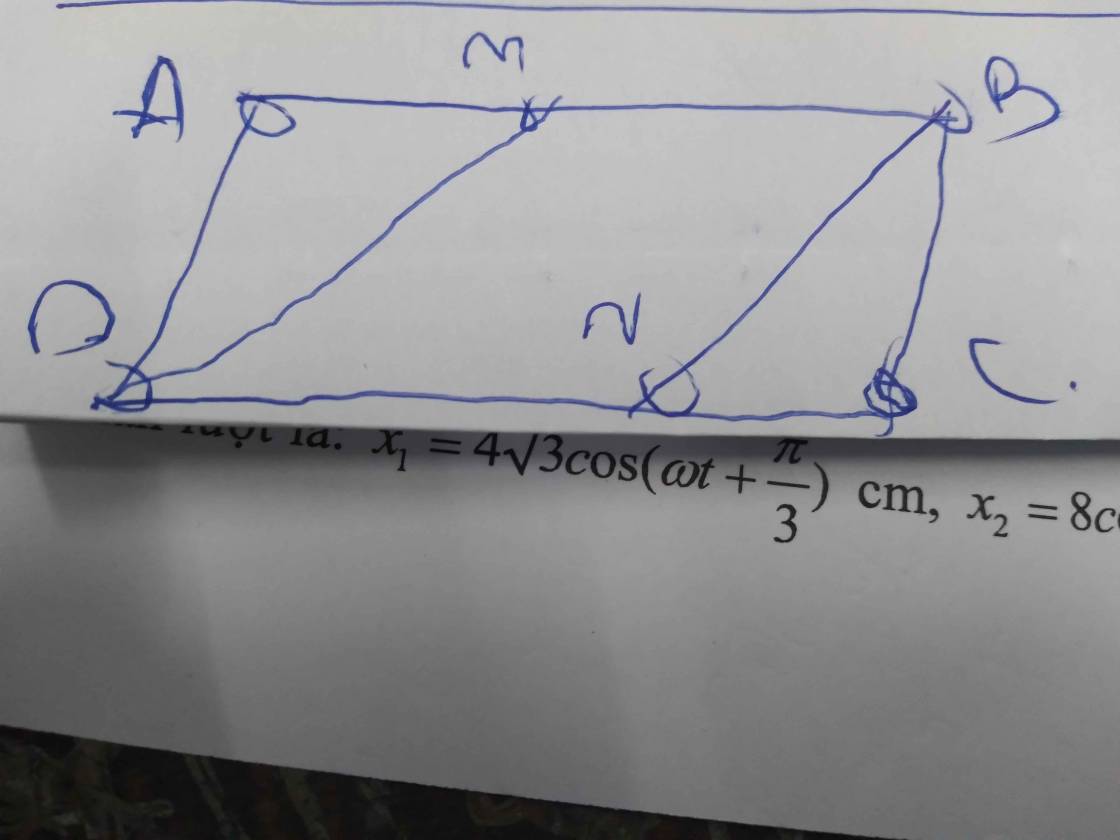
a: Ta có: \(\widehat{ADE}=\dfrac{\widehat{ADC}}{2}\)
\(\widehat{CBF}=\dfrac{\widehat{CBA}}{2}\)
mà \(\widehat{ADC}=\widehat{CBA}\)
nên \(\widehat{ADE}=\widehat{CBF}\)
Xét ΔADE và ΔCBF có
\(\widehat{ADE}=\widehat{CBF}\)
AD=BC
\(\widehat{DAE}=\widehat{BCF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
Ta có: AE+EB=AB
CF+DF=CD
mà AB=CD
và AE=CF
nên EB=DF
Xét tứ giác DEBF có
EB//DF
EB=DF
Do đó: DEBF là hình bình hành
Suy ra: DE//BF
d: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
e: Ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường\(\left(1\right)\)
Ta có: EBFD là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra AC,BD,EF đồng quy

Cách 1: Tách số hạng thứ hai
x2 – 6x + 8 = x2 – 2x – 4x + 8
= x(x – 2) – 4( x – 2)
= (x – )(x – 4).
Cách 2: Tách số hạng thứ 3
x2 - 6x + 8 = x2 – 6x + 9 – 1
= (x – 3)2 – 1 = ( x – 3 – 1)(x – 3 + 1)
= (x – 4)( x – 2).
Cách 3: x2 – 6x + 8 = x2 – 4 – 6x + 12
= ( x – 2)(x + 2) – 6(x – 2)
= (x – 2)(x – 4)
Cách 4: x2 – 6x + 8 = x2 – 16 – 6x + 24
= ( x – 4)(4 + x) – 6(x – 4)
= (x – 4)( x + 4 – 6)
= (x – 4) ( x – 2).
Cách 5 : x2 – 6x + 8 = x2 – 4x + 4 – 2x + 4
= (x – 2)2 – 2( x – 2)
= (x – 2)( x – 2 – 2)
= ( x – 2)(x – 4).