Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S A B C = 1/3 S A B C D = S/2
CN = 1/3 BC , NT // AB.
Theo tính chất đường thẳng song song cách đều ⇒ CT = 1/3 AC
△ ABC và △ BTC có chung chiều cao kẻ từ đỉnh B, đáy CT = 1/3 AC
⇒ S B T C = 1/3 S A B C = 1/3 . S/2 = S/6
△ BTC và △ TNC có chung chiều cao kẻ từ đỉnh T, cạnh đáy CN = 1/3 CB
⇒ S T N C = 1/3 S B T C = 1/3 . S/6 = S/18
S A B N T = S A B C - S T N C = S/2 - S/18 = 9S/18 - S/18 = 4S/9

A B C D M N T h
a) dt(ABMD) = dt(ABCD) - dt(CMD)
Mà dt(CMD) = 1/2 MC.h = 1/2 . 2/3 . BC .h = 1/3 dt(ABCD) = 1/3.S
(với h là đường cao hạ từ A xuống BC của hình bình hành ABCD)
Suy ra dt(ABMD) = S - 1/3 S = 2/3. S
b) dt(ABNT) = BN.h = 2/3 BC . h = 2/3 . S

△ DMC có CM = 2/3BC
Hình bình hành ABCD và ΔDMC có chung đường cao kẻ từ đỉnh D đến BC.
Gọi độ dài đường cao là h, BC = a
Ta có diện tích hình bình hành ABCD là S = a h
S D M C = 1/2 h. 2/3 a = 1/3 ah = 1/3 S
S A B M D = S A B C D - S D M C = s - 1/3 S = 2/3 S


a
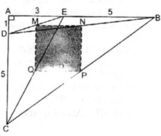
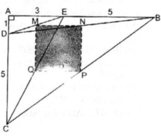
Do \(MN//BC\) nên theo định lý Thales ta có:\(\frac{AN}{NC}=\frac{AM}{MB}=\frac{MN}{BC}\)
\(\Rightarrow\frac{8}{NC}=\frac{3}{2}\Rightarrow NC=\frac{16}{3}\)
Áp dụng định Pythagoras ta có:\(AM^2+AN^2=MN^2\Rightarrow MN=\sqrt{AM^2+AN^2}=10\)
Mà \(\frac{AM}{MB}=\frac{MN}{BC}\Rightarrow\frac{3}{2}=\frac{10}{BC}\Rightarrow BC=\frac{20}{3}\)
b
Hạ \(NH\perp BC;MG\perp BC\)
Áp dụng định lý Pythagoras vào tam giác ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB^2=\sqrt{BC^2-AC^2}\Rightarrow AB=\sqrt{10-\left(\frac{16}{3}\right)^2-8^2}=\frac{2\sqrt{17}}{3}\)
Bạn áp dụng định lý Ta Lét ( do ND//AB ) rồi tính được ND
Diện tích tam giác vuông NCD sẽ tính bằng \(\frac{NC\cdot ND}{2}\) ( do đã biết được ND và NC )
Lại có \(S_{NCD}=\frac{NH\cdot CD}{2}\) rồi tính được NH.
Do NH=MG nên tính được diện tích hình bình hành BMND.Hướng là thế đấy,bạn làm tiếp nha,mik nhác quá:(

a: Xét tứ giác ABCD có
O là trung điểm chung của AC và BD
=>ABCD là hình bình hành
b: Xét ΔOAI và ΔOCN có
góc AOI=góc CON
OA=OC
góc OAI=góc OCN
=>ΔOAI=ΔOCN
=>AI=NC
=>AI=MN
mà AI//MN
nên AINM là hình bình hành
=>AM//IN