Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

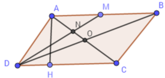
Tứ giác ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm O của mỗi đường.
Xét tam giác ABD ta có: AO và DM là hai đường trung tuyến của tam giác.
Mà AO ∩ DM = {N} => N là trọng tâm tam giác ADB.
=> AN = 2 3 DM (tính chất đường trung tuyến của tam giác)
Suy ra NM = D M 3
+) Hai tam giác AMN và ADM có cùng đường cao hạ từ A
nên S A M N S A D M = M N D M = 1 3
Mà theo câu trước SADM = 3 cm2
=> SAMN = 1 3 SADM = .3 = 1(cm2)
Đáp án cần chọn là: D

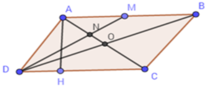
SABCD = AH.CD = 4.3 = 12(cm2)
Vì M là trung điểm của AB nên AM = 1 2 AB = 1 2 .4 = 2(cm)
Ta có chiều cao từ đỉnh D đến cạnh AM của tam giác ADM bằng chiều cao AH của hình bình hành.
=> SADM = 1 2 AH.AM = 1 2 .3.2 = 3(cm2)
Đáp án cần chọn là: A

a) Gọi H là chân đường vuông góc kẻ từ A xuống CD
Theo đề bài, ta có: AH=3(cm)
Xét hình bình hành ABCD có AH là đường cao ứng với cạnh CD(gt)
nên \(S_{ABCD}=AH\cdot CD=4\cdot3=12\left(cm^2\right)\)

a, \(S_{ABCD}\) = AH.CD
= 3.4
= 12 (\(cm^2\))
b, Ta có M là trung điểm AB
⇒ AM = \(\dfrac{AB}{2}\) = \(\dfrac{4}{2}\) = 2 (cm)
\(S_{ADM}\) = \(\dfrac{AH.AM}{2}\)
= \(\dfrac{3.2}{2}\)
= 3 (\(cm^2\))
c, Gọi O là trung điểm
c, Gọi O là trung điểm ND
Từ O kẻ OP // CD
Xét ΔNDC có: NO = OD
OP // CD
⇒ OP là đường trung bình ΔNDC
⇒ OP = \(\dfrac{1}{2}DC\) mà DC = 4 cm
⇒ OP = 2 cm
Xét ΔAMN và ΔPON có:
Góc BAC = góc APO
Góc MOP = góc AMD
AM = ON
⇒ ΔAMN = ΔPON (g.c.g)
⇒ NM = ON mà ON = \(\dfrac{1}{2}DM\)
⇒ DN = 2MN
Gọi E là trung diểm của cạnh CD. Từ E kẻ đường thẳng song song với AC cắt MD tại P
<=> EP//CN mà E là trung điểm của cạnh CD(gt) => D là trung điểm của cạnh DN =>DP=PN (1)
Ta lại có ABCD là hình bình hành =>AB=CD
Mà
+ M là trung điểm của cạnh AB
+ E là trung điểm của cạnh CD
=> AM = DE
Xét tam giác AMN và tam giác EDP có:
góc MAN = góc DEP
AM=DE
góc AMN = góc EDP
suy ra tam giác AMN = tam giác EDP (gcg) => MN= DP (2)
Từ 1 và 2 => DP=PN=MN
=> DN=2MN (điều phải chứng minh)
Chính xác 100%, chúc bạn học tốt
Gọi E là trung diểm của cạnh CD. Từ E kẻ đường thẳng song song với AC cắt MD tại P
<=> EP//CN mà E là trung điểm của cạnh CD(gt) => D là trung điểm của cạnh DN =>DP=PN (1)
Ta lại có ABCD là hình bình hành =>AB=CD
Mà
+ M là trung điểm của cạnh AB
+ E là trung điểm của cạnh CD
=> AM = DE
Xét tam giác AMN và tam giác EDP có:
góc MAN = góc DEP
AM=DE
góc AMN = góc EDP
suy ra tam giác AMN = tam giác EDP (gcg) => MN= DP (2)
Từ 1 và 2 => DP=PN=MN
=> DN=2MN (điều phải chứng minh)
Chính xác 100%, chúc bạn học tốt