Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

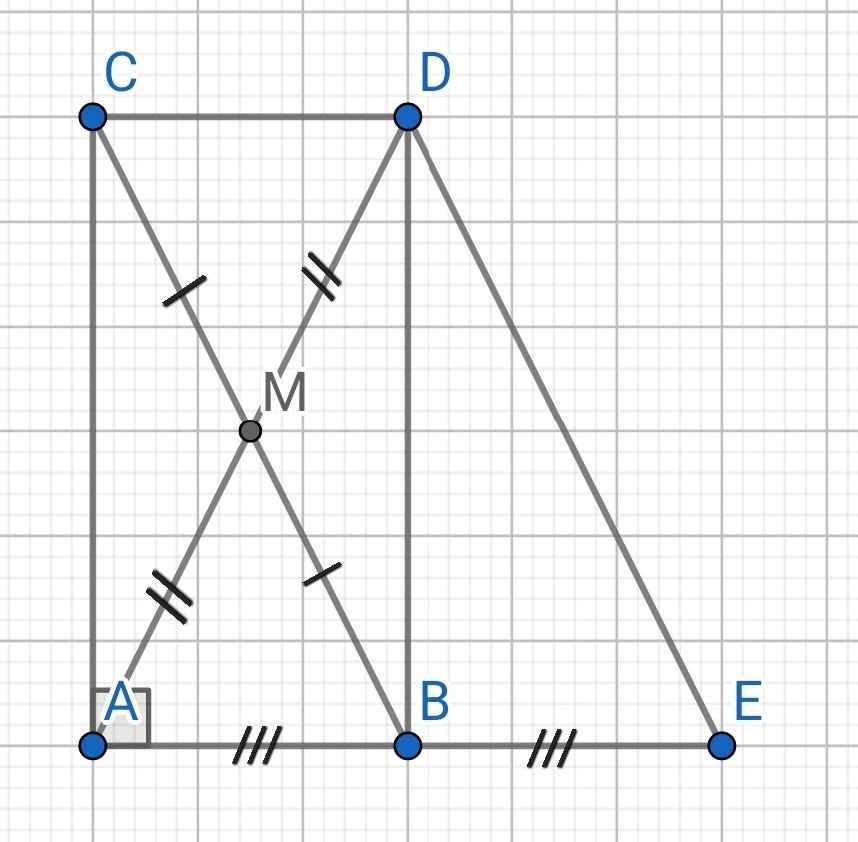 a) Tứ giác ABDC có:
a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!

Hình bạn có thể tự vẽ nha
a) Tứ giác AMCK là hình gì?Vì sao?
M,K đối xứng nhau qua I
=> I là trung điểm của MK (1)
I là trung điểm của AC (gt)(2)
(1)(2)=> AMCK là hình bình hành (3)
Tam giác ABC cân tại A có: AM là trung tuyến (gt)
=> AM vừa là trung tuyến vừa là đường cao (t/c)
=>AM vuông góc với BC
=> Góc BMC=90(4)
(3)(4)=> AMCK là hình chữ nhật(dhnb)
b) C/m ABEC là hình thoi:
AM=ME(gt)(5)
M nằm giữa A và E(6)
(5)(6)=>M là trung điểm AE(7)
M là trung điểm BC(8)
(7)(8)=> ABEC là hình bình hành(9)
AM vuông góc với BC,M thuộc AE=>AE vuông góc với BC(10)
(9)(10)=> ABEC là hình thoi (dhnb)



#Tự vẽ hình nhé bạn#
a ) Ta có :
\(\Rightarrow\)◇ABEC là hình bình hành ( vì có 2 đường chéo AE và BC cắt nhau tại trung điểm M )
b ) Xét \(\Delta\)ADE có :
\(\Rightarrow\)C là trung điểm DE