Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

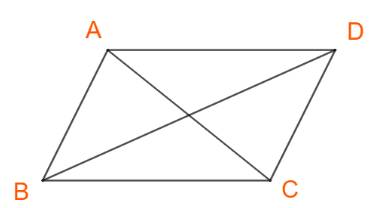
a) Áp dụng định lí cosin ta có:
\(\left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos ABC\\B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos BAD\end{array} \right.\)
Mà \(AD = BC;\cos BAD = \cos ({180^ \circ } - ABC) = - \cos ABC\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} + 2.AB.BC.\cos BAD\\B{D^2} = A{B^2} + B{C^2} - 2.AB.AD.\cos BAD\end{array} \right.\end{array}\)
Cộng vế với vế ta được:
\( A{C^2} + B{D^2} = 2\left( {A{B^2} + B{C^2}} \right)\)
b) Theo câu a, ta suy ra: \(A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - B{D^2}\)
\(\begin{array}{l} \Rightarrow A{C^2} = 2\left( {{4^2} + {5^2}} \right) - {7^2} = 33\\ \Rightarrow AC = \sqrt {33} \end{array}\)

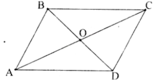
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
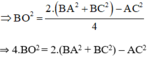
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).

Gọi O là giao của hai đường chéo
Ta có: \(\overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB}\); \(\overrightarrow{AD}=\overrightarrow{AO}+\overrightarrow{OD}=\overrightarrow{AO}-\overrightarrow{OB}\)
Suy ra : \(\overrightarrow{AB}.\overrightarrow{AD}=AO^2-OB^2=3^2-4^2=-7\)
\(\Leftrightarrow AB^2.AD^2=49\)\(\Leftrightarrow AD^2=\dfrac{49}{16}\Leftrightarrow AD=\dfrac{7}{4}\)

Xét ΔABD có
\(cosBAD=\dfrac{AB^2+AD^2-BD^2}{2\cdot AB\cdot AD}\)
=>\(8^2+6^2-BD^2=2\cdot8\cdot6\cdot cos60=48\)
=>\(BD^2=100-48=52\)
=>\(BD=2\sqrt{13}\left(cm\right)\)
Xét ΔBAC có \(cosABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
=>\(8^2+6^2-AC^2=2\cdot8\cdot6\cdot cos120=-48\)
=>\(AC^2=148\)
=>\(AC=2\sqrt{37}\left(cm\right)\)

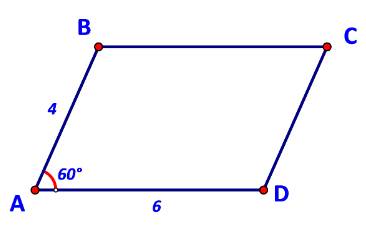
a) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)
c) Áp dụng định lí cosin cho tam giác ABD ta có:
\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)

Lời giải:
\(AC^2+BD^2=(\overrightarrow{AC})^2+(\overrightarrow{BD})^2\)
\(=(\overrightarrow{AB}+\overrightarrow{AD})^2+(\overrightarrow{BA}+\overrightarrow{BC})^2\)
\(=AB^2+AD^2+AB^2+BC^2+2\overrightarrow{AB}.\overrightarrow{AD}+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=2(a^2+b^2)+2\overrightarrow{AB}.\overrightarrow{AD}-2\overrightarrow{AB}.\overrightarrow{AD}=2(a^2+b^2)\)
