Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sử dụng đường trung bình, ta có: KN = 1/2 AB, NI = 1/2 CD , IM = 1/2 AB , MK = 1/2 CD
Mà AB = CD (gt)
\(\Rightarrow KN=NI=IM=MK\)
\(\Rightarrow KNIM\)là hình thoi
Do đó: MN là tia phân giác của \(\widehat{IMK}\)(tính chất hình thoi)
Chúc bạn học tốt.

Bài 22 :
Vì ABCD là hình bình hành
=> AB = DC
Mà M là trung điểm AB
=> AM = MB
Mà N là trung điểm DC
=> DN = NC
=> AM = DN
Mà AB//DC
=> DN//AM
=> AMND là hình bình hành
Chứng minh tương tự ta có : MBCN là hình bình hành

Hình bạn tự vẽ nha!
a, ta có:
Góc A=Góc D=90°(gt)<=>AD_|_DC
BH_|_DC
=>BH//AD
ABCD là hình thang nên AB//CD
=>Tứ giác ABHD là hình chữ nhật.
b,Do ABHD là hình chữ nhật, nên:
AB=HD=3cm
CD=6cm=>HC=6-3=3 cm
Do BH_|_CD(gt)=>góc BHC=90°
=>tam giác BHC vuông tại H
Xét tam giác vuông BHC:
Theo định lý pitago trong tam giác vuông thì:
BC^2=HC^2+BH^2
=>BH^2=BC^2-HC^2=(5)^2-(3)^2=16
=>BH=4 cm
=>Diện tích hình chữ nhật ABHD là:
3.4=12 cm2
c,Do M là M là trung điểm của BC nên:
MB=MC=BC/2=5/2=2,5cm
Do N đối xứng với M qua E (gt)nên:
EM=EN
Đường chéo AH^2=AD^2+DH^2=25cm
=>AH=5cm=>EH=5/2=2,5cm
=>Tứ giác ABCHH=NMCD vì MC=ND=BC/2=2,5 cm
EM+EN=2AB=6 cm
AB//HC=3cm;BC//AH=5cm
=>NM//DC=6cm
==> Tứ giác NMCD là hình bình hành
d,bạn tự chứng minh (khoai quá)

Bài 2:
AK=AB/2
CI=CD/2
mà AB=CD
nên AK=CI
Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
=>AC cắt KI tại trung điểm của mỗi đường(1)
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,KI,BD đồng quy
Bài 1:
a: \(\widehat{ADE}=\widehat{EDF}=\dfrac{1}{2}\cdot\widehat{ADC}\)
\(\widehat{ABF}=\widehat{CBF}=\dfrac{1}{2}\cdot\widehat{ABC}\)
mà \(\widehat{ADC}=\widehat{ABC}\)
nên \(\widehat{ADE}=\widehat{EDF}=\widehat{ABF}=\widehat{CBF}\)
Xét ΔEAD và ΔFCB có
\(\widehat{A}=\widehat{C}\)
AD=CB
\(\widehat{EDA}=\widehat{FBC}\)
Do đó: ΔEAD=ΔFCB
=>\(\widehat{AED}=\widehat{CFB}\)
=>\(\widehat{EDF}=\widehat{CFB}\)
mà hai góc này đồng vị
nên DE//BF
b: Xét tứ giác DEBF có
DE//BF
BE//DF
Do đó: DEBF là hình bình hành

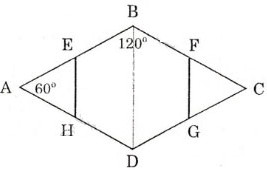
ABCD là hình thoi,  =
=  nên
nên 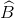 =
=  ,
,  =
=  .
.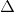 EAH là tam giác đều (vì tam giác cân có một góc
EAH là tam giác đều (vì tam giác cân có một góc  ) nên
) nên 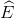 =
=  ,
,  =
=  . Cũng thế
. Cũng thế  =
=  ,
,  =
=  .
.
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều

ABCD là hình thoi,  =
=  nên
nên 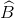 =
=  ,
,  =
=  .
.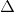 EAH là tam giác đều (vì tam giác cân có một góc
EAH là tam giác đều (vì tam giác cân có một góc  ) nên
) nên 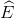 =
=  ,
,  =
=  . Cũng thế
. Cũng thế  =
=  ,
,  =
=  .
.
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều

Xin phép ad cho em tách ạ,nguyên 1 câu khá là dài,hihi

