Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C E M D
a) ta có: A là trung điểm BD(AD=AB) mà EA=\(\dfrac{1}{3}\)AC nên E là trọng tâm tam giác DCB
ta lại có BE cắt CD tại M nên BM là trung tuyến tam giác DBC nên M là trung điểm BC
b) ta có M là trung điểm DC, A là trung điểm DC nên AM là đường trung bình tam giác DBC
\(\Rightarrow AM=\dfrac{BC}{2}=\dfrac{1}{2}BC\)

A) Ta có AB2 + AC2 = BC2 => AB2 = BC2 - AC2 = 100 - 36 => AB = 8cm
B) AM = BM (Do CM là trung tuyến của tam giác ABC)
CM = MD (Theo đề bài)
góc AMC = BMD (hai góc đối đỉnh)
=> Tam giác MAC = tam giác MBD (cgc)
=> AC = BD (Hai cạnh tương ứng của hai tam giác bằng nhau)
C) Ta có BC + BD > CD
=> BC + AC > 2 CM

theo t/c góc ngoài tam giác ACB ta có:
ACM=CAB+ABC=180-2ABC+ABC=180-ABC
ABN=180-MAB(do BN//AM)
=180-ABC=> DPCM

a/Áp dụng định lí Pytago và tam giác ABC vuông tại A:
BC2=AB2+AC2
=>AC2=BC2-AB2=102-62=100-36=64
=> AC=\(\sqrt{64}=8cm\)
b/ Xét tam giác ABC và tam giác ADC có:
AC chung
góc BAC=DAC=90 độ
AD=AB(gt)
=> Tam giác ABC=tam giác ADC(c-g-c)

gọi H, K là trung điểm AB, AC thì HK là đường tb của hình thang DMNE. HK=(DM+EN)/2
Bc=2HK

C/m 3 điểm thẳng hàng là tìm trọng tâm của tam giác đóa pạn, có trọng tâm ròi =>D,M.F thẳng hàng

Đáp án A
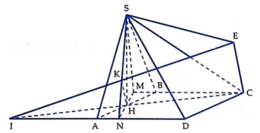
Gọi φ là góc giữa SC và (SAD), N là giao điểm của HM và AD, K là hình chiếu vuông góc của H trên SN, I là giao điểm của HC với AD. Gọi E là điểm đối xứng với I qua K.
Ta có M B = 1 4 B C = a 2 , H B = a , H B M ^ = B A D ^ = 60 °
⇒ H M = H B 2 + M B 2 − 2 H B . M B . c o s H B M ^
⇒ H M = a 2 + a 2 4 − 2 a . a 2 . cos 60 ° = 3 2 a
⇒ H M 2 + M B 2 = 3 2 a 2 + a 2 2 = a 2 = H B 2
⇒ Δ H M B vuông tại M
⇒ H M ⊥ M B hay M N ⊥ B C .
Vì S H ⊥ A D do S H ⊥ A B C D M N ⊥ A D do M N ⊥ B C ⇒ A D ⊥ S M N ⇒ A D ⊥ H K , mà H K ⊥ S N nên H K ⊥ S A D . Lại có HK là đường trung bình của Δ I C E nên H K // C E . Suy ra C E ⊥ S A D tại E và SE là hình chiếu của SC trên mặt phẳng (SAD).
Vậy φ = S C , S A D ^ = S C , S E ^ = C S E ^ .
Đặt S H = x , x > 0 . Do Δ S H N vuông tại H có HK là đường cao nên ta có
1 H K 2 = 1 S H 2 + 1 H N 2 ⇒ H K = S H . H N S H 2 + H N 2 = 3 a x 4 x 2 + 3 a 2 ⇒ C E = 2 H K = 2 3 a x 4 x 2 + 3 a 2
Do Δ S H C vuông tại H nên
S C = S H 2 + H C 2 = S H 2 + H M 2 + M C 2 = x 2 + 3 2 a 2 + 5 a 2 2 = x 2 + 7 a 2
Δ S E C vuông tại E nên sin φ = sin C S E ^ = E C S C = 2...

a: Xét tứ giác ABDE có
M là trung điểm của AD
M là trung điểm của BE
Do đó: ABDE là hình bình hành
Suy ra: AE=BD
b: Xét tứ giác AFDC có
M là trung điểm của AD
M là trung điểm của CF
Do dó: AFDC là hình bình hành
Suy ra: FA//DC
hay FA//BC
c: Ta có: AF//BC
AE//BC
mà AE,AF có điểm chung là A
nên A,E,F thẳng hàng
CN = 3,5 cm