Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) hình bình hành ABCD có:
O là giao điểm của AC và BD
=> O là trung điểm của AC và BD
xét tam giác AOM và tam giác NOC có:
AO= CO
góc A² = góc C¹ (so le trong)
góc O¹=góc O² (đối đỉnh)
=> tam giác AOM=tam giác CON(g.c.g) => OM =ON
=> M đối xứng với N qua O
b) tam giác AOM= tam giác CON nên
=> AM= CN, AM // CN
=> tứ giác AMNC là hình bình hành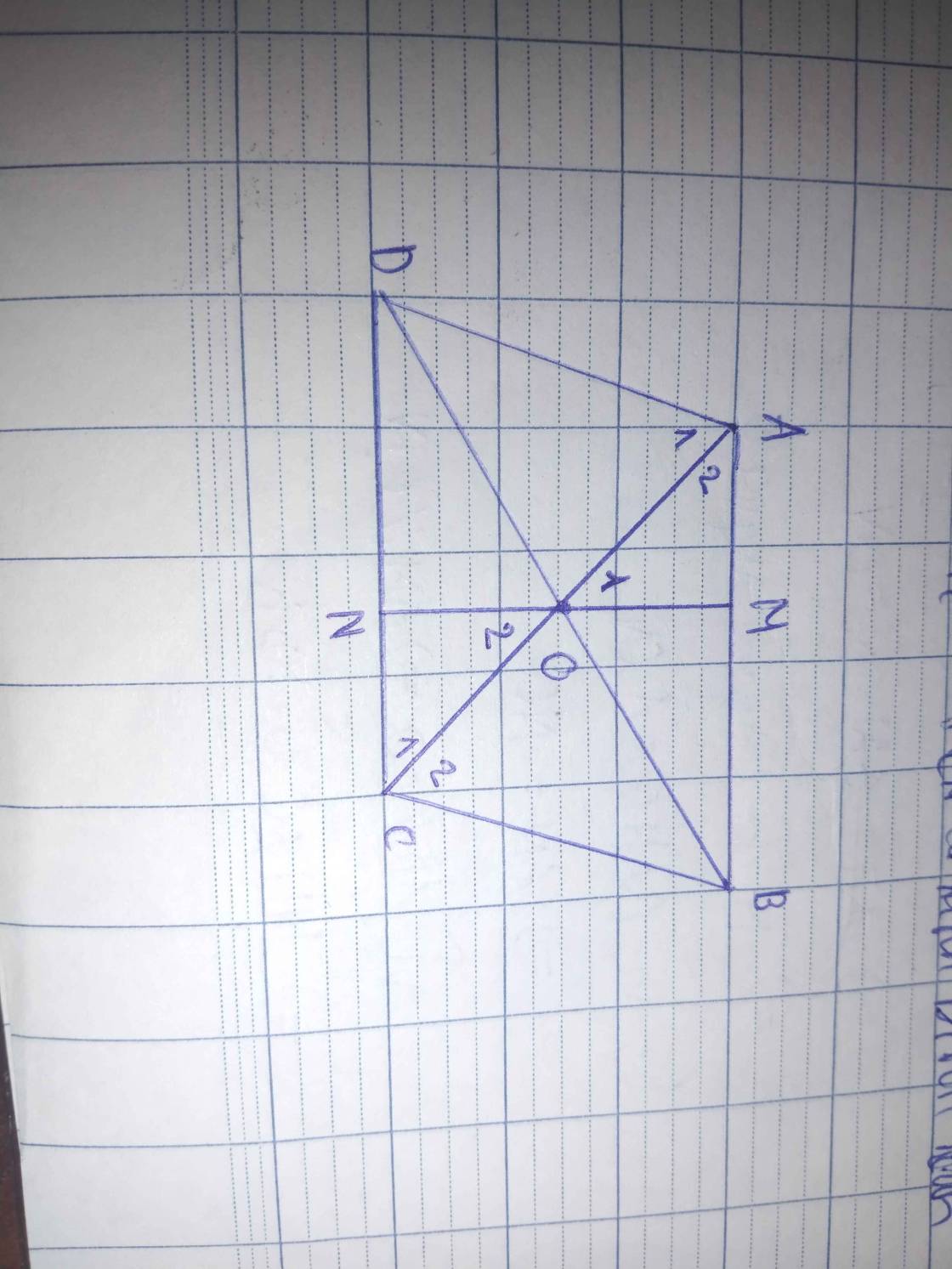 
a: Xét ΔMAO và ΔNCO có
\(\widehat{MAO}=\widehat{NCO}\)
OA=OC
\(\widehat{AOM}=\widehat{CON}\)
Do đó: ΔMAO=ΔNCO
Suy ra: MO=NO
hay M đối xứng với N qua O
a)
Do ABCD là hình thoi :
=> AB // CD=) AM // CN
Do AM // CN
=> \(\widehat{MAO}=\widehat{NCO}\) ( 2 góc so le trong )
Do ABCD là hình thoi:
Mà O là giao điểm của 2 đường chéo
=> AO = CO ( vì hình thoi có tất cả các tính chất hình bình hành ) => O là trung điểm của AC
Xét tam giác AOM và tam giác CON có :
\(\widehat{AOM}=\widehat{CON}\)( đối đỉnh )
AO = CO
\(\widehat{MAO}=\widehat{NCO}\)(chứng minh trên)
=> Δ AOM = Δ CON ( g-c-g )
b) Do Δ AOM = Δ CON ( chứng minh phần a)
=) OM = ON (2 cạch tương ứng)
=> O là trung điểm của MN
Xét tứ giác AMCN có :
2 đường chéo AC và MN cắt nhau tại trung điểm O
=> AMCN là hình bình hành
Câu 20:
a: \(2x^3-8x^2+8x=2x\left(x-2\right)^2\)
b: \(2xy+2x+yz+z=\left(y+1\right)\left(2x+z\right)\)
c: \(x^2+2x+1-y^2=\left(x+1-y\right)\left(x+1+y\right)\)
Cau 20:
a: \(2x^3-8x^2+8x=2x\left(x-2\right)^2\)
b: \(2xy+2x+yz+z=\left(y+1\right)\left(2x+z\right)\)
c: \(x^2+2x+1-y^2=\left(x+1-y\right)\left(x+1+y\right)\)