Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
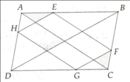
Áp dụng định lý Thalès, ta có:
HE // BD \(\Rightarrow\frac{AH}{AD}=\frac{AE}{AB}\)(1)
EF // AC \(\Rightarrow\frac{AE}{AB}=\frac{FC}{BC}\)(2)
FG // BD \(\Rightarrow\frac{FC}{BC}=\frac{GC}{DC}\)(3)
Từ (1),(2),(3) suy ra \(\frac{AH}{AD}=\frac{GC}{DC}\Rightarrow AH.CD=AD.CG\left(đpcm\right)\)
Sửa đề: Cho hình thang ABCD có AB//CD
a: Xét ΔADC có OM//DC
nên \(\frac{AM}{AD}=\frac{AO}{AC}\left(1\right)\)
Xét ΔBAC có ON//AB
nên \(\frac{OC}{OA}=\frac{CN}{NB}\)
=>\(\frac{AO}{OC}=\frac{BN}{NC}\)
=>\(\frac{AO}{OC+OA}=\frac{BN}{BN+NC}\)
=>\(\frac{AO}{AC}=\frac{BN}{BC}\left(2\right)\)
Từ (1),(2) suy ra \(\frac{AM}{AD}=\frac{BN}{BC}\)
b: Xét tứ giác DMOE có
MO//DE
OE//MD
Do đó: DMOE là hình bình hành
=>DM=OE; DE=OM
Xét ΔADC có MO//DC
nên \(\frac{MO}{DC}=\frac{AM}{AD}\)
c: Xét ΔBDC có ON//DC
nên \(\frac{ON}{DC}=\frac{BN}{BC}\)
mà \(\frac{MO}{DC}=\frac{AM}{AD}\)
và \(\frac{BN}{BC}=\frac{AM}{AD}\)
nên OM=ON(1)
Xét tứ giác FCNO có
FC//NO
FO//NC
Do đó: FCNO là hình bình hành
=>FC=ON(2)
Từ (1),(2) suy ra FC=OM
mà OM=DE
nên FC=DE
d: Xét ΔDAB có OM//AB
nên \(\frac{OM}{AB}=\frac{DM}{DA}\)
Xét ΔADC có OM//DC
nên \(\frac{OM}{DC}=\frac{AM}{AD}\)
\(\frac{OM}{AB}+\frac{OM}{DC}=\frac{DM}{DA}+\frac{AM}{AD}=1\)
=>\(OM\left(\frac{1}{AB}+\frac{1}{DC}\right)=1\)
=>\(\frac{1}{AB}+\frac{1}{DC}=\frac{1}{OM}=\frac{2}{MN}\)
a) gọi N là giao điểm của EF và AC
ta có \(DI//EF\Rightarrow\widehat{AID}=\widehat{ENC}\)(so le trong)
\(BK//EF\Rightarrow\widehat{CKB}=\widehat{ENC}\) (đồng vị)
do đó \(\widehat{AID}=\widehat{CKB}\)
Ta lại có \(\widehat{ADI}=180^o-\widehat{AID}-\widehat{IAD}\)
\(\widehat{CBK}=180^o-\widehat{CKB}-\widehat{KCB}\)
\(\widehat{AID}=\widehat{CKB}\) (cmt)
\(\widehat{IAD}=\widehat{KCB}\) (vì AB // CD)
nên \(\widehat{ADI}=\widehat{CBK}\)
Xét tam giác ADI và tam giác CBK có
\(\widehat{ADI}=\widehat{CBK}\)
AD = BC (vì ABCD là hình bình hành)
\(\widehat{IAD}=\widehat{KCB}\) (vì AB // CD)
do đó tam giác ADI = tam giác CBK (g . c . g)
=> AI = CK (2 cạnh tương ứng)