Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
Suy ra:AN//CM

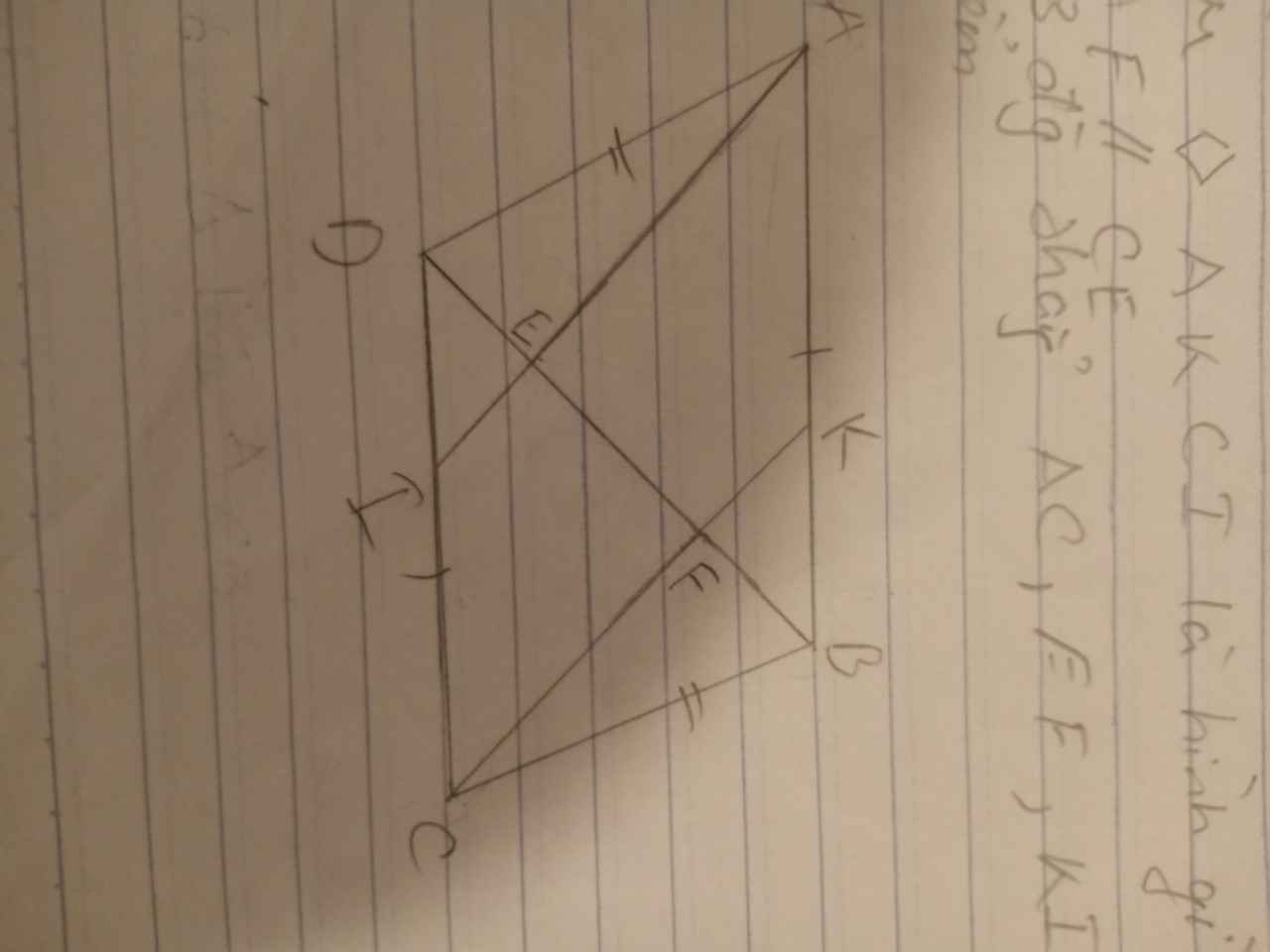
Đầu bài vô lí qua CK kẻ đg thg vuông BD tại F , cắt AC tại K
CK nào???
1: Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔAED=ΔCFB
Suy ra: AE=CF
Ta có: AE\(\perp\)BD
CF\(\perp\)BD
Do đó: AE//CF

a.
xét 2 tam giác ABD và CBD có các cặp cạnh tương ứng bằng nhau( vì hình bình hành)
=>tgiac ABD = tgiac CBD
=> đường cao AE = CF( đường cao tương ứng cũng bằng nhau) (1)
ta lại có:AE vuong goc với BD, CF vuong góc với BD => AE //CF (2)
từ 1 và 2 => AECF là hình bình hành
b.
xét 2 tam giác AID và tam giác CBK
có BC = AD( cạnh hbh) (1)
góc ADC = góc CBA ( 2 góc đối hbh) (2)
gọi:
M là giao điểm của CK và AD
N là giao điểm của AI và BC
ta có ANCM là hbh vì có các cặp cạnh song song với nhau
=> góc BCM = góc NAD (3)
từ 1,2 và 3 => tam giác BCK = tgiác DAI ( goc - canh -goc)
=> AI = CK (cpcm)
c.
xét 2 tam giác vuông ABE và CDF
ta có:
AB = CD ( 2 cạnh đối hbh ABCD)
AE = CF (2 cạnh đối hbh AECF)
=> tgiác ABE = tgiác CDF
=> BE =CF (dpcm)

Bài 3:
a: Ta có: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
Hình thang BDEC có \(\widehat{DBC}=\widehat{ECB}\)
nên BDEC là hình thang cân
b: Để BD=DE=EC thì BD=DE và DE=EC
BD=DE thì ΔDBE cân tại D
=>\(\widehat{DBE}=\widehat{DEB}\)
mà \(\widehat{DEB}=\widehat{EBC}\)(hai góc so le trong, DE//BC)
nên \(\widehat{DBE}=\widehat{EBC}\)
=>\(\widehat{ABE}=\widehat{EBC}\)
=>BE là phân giác của góc ABC
=>E là chân đường phân giác kẻ từ B xuống AC
Xét ΔEDC có ED=EC
nên ΔEDC cân tại E
=>\(\widehat{EDC}=\widehat{ECD}\)
mà \(\widehat{EDC}=\widehat{DCB}\)(hai góc so le trong, DE//BC)
nên \(\widehat{ECD}=\widehat{DCB}\)
=>\(\widehat{ACD}=\widehat{BCD}\)
=>CD là phân giác của góc ACB
=>D là chân đường phân giác từ C kẻ xuống AB
Bài 2:
a: Ta có: ABCD là hình bình hành
=>AB//CD và AB=CD(1)
Ta có: M là trung điểm của AB
=>\(AM=MB=\dfrac{AB}{2}\left(2\right)\)
Ta có: N là trung điểm của CD
=>\(NC=ND=\dfrac{CD}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra AM=MB=NC=ND
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b: Ta có AMCN là hình bình hành
=>AN//CM
Xét ΔDFC có
N là trung điểm của DC
NE//FC
Do đó: E là trung điểm của DF
=>DE=EF(4)
Xét ΔABE có
M là trung điểm của BA
MF//AE
Do đó: F là trung điểm của BE
=>BF=FE(5)
Từ (4) và (5) suy ra BF=FE=ED

CM: a) Xét t/giác AHD và t/giác CKB
có: AD = BC (Vì ABCD là HBH)
\(\widehat{AHD}=\widehat{CKB}=90^0\)(gt)
\(\widehat{ADH}=\widehat{KBC}\)(slt của AD // BC)
=? t/giác AHD = t/giác CKB (ch - gn)
=> AH = CK (2 cạnh t/ứng)
b) Xét tứ giác AHCK có AH // CK (Vì cùng vuông góc với BD)
AH = CK (cmt)
=> AHCK là HBH
c) Xét t/giác ADH và t/giác BDM
có: \(\widehat{MDB}\):chung
\(\widehat{AHD}=\widehat{M}=90^0\) (gt)
=> t/giác ADH đồng dạng t/giác BDM (g.g)
=> \(\frac{AD}{BD}=\frac{DH}{DM}\) => AD.DM = BD.DH (1)
Xét t/giác DCK và t/giác DBN
có \(\widehat{BDN}\):chung
\(\widehat{DKC}=\widehat{N}=90^0\)(gt)
=> t/giác DCK đồng dạng t/giác DBN
=> \(\frac{DC}{DB}=\frac{DK}{DN}\)=> DC. DN = DB.DK (2)
Từ (1) và (2) công vế theo vế, ta được:
DA.DM + DC.DN = BD. DH + DB.DK = BD(DH + DK)
vì DH = BK (vì t/giác ADH = t/giác CBK)
=> DA.DM + DC.DN = BD. (BK + DK) = BD2

Đầu bài vô lí qua CK kẻ đg thg vuông BD tại F , cắt AC tại K
1: Ta có: AE\(\perp\)BD
CF\(\perp\)BD
Do đó: AE//CF
Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔAED=ΔCFB
Suy ra: AE=CF

a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔAHD=ΔCKB
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
b: Ta có: AHCK là hình bình hành
nên Hai đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của HK
nên O là trung điểm của AC
hay A,O,C thẳng hàng
Ta có:
ABCD là hình bình hành => AB//CD ( tính chất hình bình hành )
vì AB//CD ==> Góc AEC + Góc EAK = 180 độ ( trong cùng phía )
=> góc EAK = 90 độ
Xét Tứ giác AKCH có:
góc K vuông
Góc E vuông
Góc EAK vuông
=> tứ giác AKCH là hình chữ nhật