PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
28 tháng 6 2020
a.Xét tam giác AMH và tam giác NMB có
MA = MN [ gt ]
góc AMH = góc NMB [ đối đỉnh ]
HM = BM [ gt ]
Do đó ; tam giác AMH = tam giác NMB [ c.g.c ]
\(\Rightarrow\)góc AHM = góc NBM
mà bài cho góc AHM = 90độ
\(\Rightarrow\)góc NBM = 90độ
Vậy NB vuông góc với BC
b.Theo câu a ; tam giác AMH = tam giác NMB
\(\Rightarrow\)AH = NB [ cạnh tương ứng ]
Mặt khác ; Xét tam giác AHB vuông tại H có
AB lớn hơn AH
\(\Rightarrow\)AB lớn hơn NB
TB
4 tháng 2 2018
Giải
Kẻ đoạn thẳng AM. Xét tam giác MAC. Chứng minh tương tự như bài 1.4 ta có MN < a, trong đó a là đoạn lớn nhất trong hai đoạn thẳng MA và MC. Nếu ta chứng minh được
MA < AC và MC < AC thì sẽ suy ra được a < AC, từ đó có MN < AC.
Trong tam giác ABC có AB ≤ AC, M ∈ BC (M ≠ B, M ≠ C); Chứng minh tương tự bài 1.4, ta có AM < AC. Mặt khác MC < BC ≤ CA. Vậy a < AC, suy ra MN < AC.
19 tháng 2 2019
bạn ơi cách này trong phần giải đằng sau sách bài tập toán 7 mà !!!
4 tháng 3 2016
B A C M N
Áp dụng bất đẳng thức tam giác cho tam giác CMN ta có:
\(CN+CM>MN\)
Vì N nằm trên BC nên CN<BC
Vì M nằm trên AC nên CM<AC
=>\(BC+AC>CM+CN>MN\)
Đến đây tự giải tiếp thì dễ rồi
MC
26 tháng 1 2019
a) Có: \(\left\{{}\begin{matrix}\widehat{MAC}=90^0+\widehat{BAC}\left(\widehat{MAB}=90^0\right)\\\widehat{BAN}=90^0+\widehat{BAC}\left(\widehat{CAN}=90^0\right)\end{matrix}\right.\Rightarrow\widehat{MAC}=\widehat{BAN}\)
- Xét \(\Delta AMC\) và \(\Delta ABN\) có \(\left\{{}\begin{matrix}AM=AB\left(gt\right)\\\widehat{MAC}=\widehat{BAN}\left(cmt\right)\\AN=AC\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AMC=\Delta ABN\left(c.g.c\right)\)
Vậy \(\Delta AMC=\Delta ABN\)
b) - Gọi D là giao điểm của CM và AB; K là giao điểm của CM và BN.
- Có: \(\Delta AMC=\Delta ABN\) (theo a)
\(\Rightarrow\widehat{AMC}=\widehat{ABN}\) hay \(\widehat{AMD}=\widehat{HBK}\)
- Xét \(\Delta AMD\) vuông tại A có \(\widehat{AMD}+\widehat{ADM}=90^0\) (định lý tam giác vuông)
Mà \(\widehat{AMD}=\widehat{DBK}\left(cmt\right)\); \(\widehat{ADM}=\widehat{BDK}\)(hai góc đối đỉnh)
Suy ra \(\widehat{DBK}+\widehat{BDK}=90^0\)
- Xét \(\Delta BDK\) có \(\widehat{DBK}+\widehat{BDK}+\widehat{BKD}=180^0\) (định lý tổng 3 góc)
\(\Rightarrow90^0+\widehat{BKD}=180^0\)
\(\Rightarrow\widehat{BKD}=90^0\)
hay \(BN\perp CM\)
Vậy \(BN\perp CM\)
c) Kẻ \(ME\perp AH\) tại E; \(NF\perp AH\) tại F. Gọi O là giao điểm của MN và AH.
- Có: \(\widehat{BAH}+\widehat{MAB}+\widehat{MAE}=180^0\) (Ba điểm H; A; E thẳng hàng)
\(\Rightarrow\widehat{BAH}+90^0+\widehat{MAE}=180^0\)
\(\Rightarrow\widehat{BAH}+\widehat{MAE}=90^0\left(1\right)\)
- Xét \(\Delta ABH\) vuông tại H có \(\widehat{BAH}+\widehat{ABH}=90^0\) (định lý tam giác vuông) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) suy ra \(\widehat{MAE}=\widehat{ABH}\)
- Xét \(\Delta MAE\) vuông tại E và \(\Delta ABH\) vuông tại H có \(\left\{{}\begin{matrix}AM=AB\left(gt\right)\\\widehat{MAE}=\widehat{ABH}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MAE=\Delta ABH\) (cạnh huyền - góc nhọn)
\(\Rightarrow ME=AH\) (hai cạnh tương ứng)
Chứng minh tương tự, ta có: \(\Delta AFN=\Delta CHA\) (cạnh huyền - góc nhọn)
\(\Rightarrow NF=AH\) (hai cạnh tương ứng)
- Có \(\left\{{}\begin{matrix}ME=AH\left(cmt\right)\\NF=AH\left(cmt\right)\end{matrix}\right.\Rightarrow ME=NF\)
- Có: \(\left\{{}\begin{matrix}ME\perp EF\left(vẽ\right)\\NF\perp EF\left(vẽ\right)\end{matrix}\right.\Rightarrow ME//NF\) (quan hệ vuông góc - song song)
\(\Rightarrow\widehat{OME}=\widehat{ONF}\) (hai góc so le trong)
- Xét \(\Delta OME\) vuông tại E và \(\Delta ONF\) vuông tại F có \(\left\{{}\begin{matrix}ME=NF\\\widehat{OME}=\widehat{ONF}\end{matrix}\right.\left(cmt\right)\Rightarrow\Delta OME=\Delta ONF\left(cgv-gnk\right)\)
\(\Rightarrow OM=ON\)(hai cạnh tương ứng)
hay AH đi qua trung điểm O của MN
Vậy AH đi qua trung điểm của MN
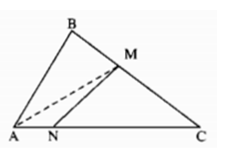
Nối BN.
+ Ta có: AM < AB
Mà NM, NB là các đường xiên ứng với hình chiếu AM, AB
⇒ NM < NB (1)
+ Lại có AN < AC.
Mà BN, BC là các đường xiên ứng với hình chiếu AN, AC
⇒ BN < BC (2)
Từ (1) và (2) suy ra: MN < BC