Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Định lí:
+ Nếu các đường thẳng song song cách đều cắt một đường thằng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
+ Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
⇒ EF = FG = GH
Chọn đáp án C.

Định lí:
+ Nếu các đường thẳng song song cách đều cắt một đường thằng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
+ Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
⇒ EF = FG = GH
Chọn đáp án C.

Hih e tự vẽ nha:
a) Vì DM//BE nên tứ giác BDME là hình thang.
Lại có :\(\widehat{B}=\widehat{C}=60\)( tam giác ABC đều)
và \(\widehat{BEM}=\widehat{C}=60\)(Vì DE//AC và ACB=90 độ)
=>\(\widehat{BEM}=\widehat{B}=60\)
=>Tứ giác BDME là htc.
T/tự cho các hình còn lại.
b)Xét tam giác BDM và EMD:
BD=ME( BDME là htc)
góc BDM=góc EMD(Vì DM//BE và góc BEM=góc B=60 độ)
DM là cah chug
=> tg BDM=tg EMD (cgc)
=>BM=DE
C/m t/tự đối vói các tg AFD=AMF; tg CEM=tg FME
=> AM=DF;CM=EF
=>BM+AM+CM=DE+DF+EF= Chu vi của tam giác DEF
c) Ở câu a/ ta đã có góc B= góc E=60 nên suy ra đc các góc còn lại của htc BDME bằng 120 độ
T/tự cho 2 htc còn lại suy ra đc cả 3 góc đều =120 độ nên chúng = nhau
M A B C D E F
a, Chứng minh các tứ giác BDME,CFME,ADMF là các hình hang cân.
Ta có : MD//BC\(\Rightarrow\)BDME là hình thang cân .(1)
ME//AC\(\Rightarrow\widehat{MEB}=\widehat{ACB}\)(hai góc đồng vị )
mà \(\widehat{ACB}=\widehat{ABC}=60^o\)(do tam giác ABC đều)
\(\Rightarrow\widehat{MEB}=\widehat{ABC}=60^o\)(2)
Từ (1) và (2) => tứ giác BDME là hình thang cân.
Chứng minh tương tự ta cũng có : tứ giác CFME và ADMF là các hình thang cân.
b,Chứng minh chu vi của tam giác DEF bằng tổng các khoảng cách từ M đến các đỉnh của tam giác ABC . \(\left(P_{DME}=MB+MA+MC\right)\)
Ta có : \(P_{DEF}=DE+DF+EF\)
Lại có tứ giác BDME là hình thang cân (cmt) => DE = MB.
tứ giác CFME là hình thang cân (cmt)=> MC=EF
tứ giác DMF là hình thang cân (cmt)=> MA =DF.
\(\Rightarrow P_{DEF}=MA+MB+MC\)
=> đpcm.
c,Chứng minh \(\widehat{DME}=\widehat{DMF}=\widehat{EMF}\)
Trong hình thang cân BDME có : \(\widehat{DBE}=60^o\)
mà \(\widehat{DME}+\widehat{DBE}=180^o\Rightarrow\widehat{DME}=180^o-\widehat{DBE}=180^o-60^o=120^o\)
Chứng minh tương tự ta có : \(\widehat{DMF}=120^o;\widehat{EMF}=120^o\)
=>\(\widehat{DME}=\widehat{DMF}=\widehat{EMF}=120^o\)(đpcm)
Mình giải chi tiết rùi đấy nhé nếu có j hk hiểu cứ nhắn tin cho mk mk sẽ giải thích cho nhé.
Nên nhớ hình vẽ chỉ mang tính chất minh họa . Mình vẽ hình cho mấy bạn nhìn vô cho dể hiểu thôi chứ chưa chuẩn lắm đâu mấy bạn tự vẽ hình cho đẹp nhé ai thấy hay thì k cho mk nhé . CẢM ƠN NHIỀU .

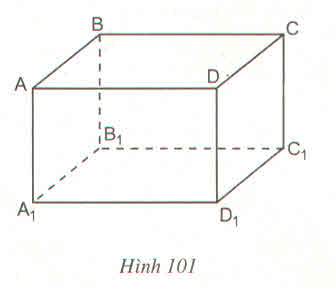
a. Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a sai.
b. Hai đường thẳng AA1 và BC không có điểm chung nhưng chúng không song song
Vậy mệnh đề b sai.

a: Xét ΔBAC có DF//AC
nên BF/FA=BD/DC=1/2
=>BF=1/2FA
=>AF/AB=2/3
Xét ΔCAB có DE//AB
nên CD/CB=CE/CA
=>CE/CA=2/3
=>CE=2/3CA
=>AE=1/3CA
=>AE/CE=1/2
=>AE/AC=1/3
b: \(\dfrac{AE}{EM}=\dfrac{AE}{\dfrac{1}{2}\cdot AC}=\dfrac{AE}{AC}\cdot\dfrac{1}{\dfrac{1}{2}}=\dfrac{1}{3}\cdot2=\dfrac{2}{3}=\dfrac{AF}{FB}\)
=>EF//BM

Gt và câu c viết nhầm phải không bạn? Trung tuyến BD,CE,AM chứ. Còn câu b phải qua B kẻ đường thẳng // FD nhỉ? Nếu thế thì lời giải thế này
(lời giải hơi dài tí)
*Xét tứ giác DEMC:
\(ED=\frac{1}{2}BC\)(cma)
\(CM=\frac{1}{2}BC\)(gt)
\(\Rightarrow ED=CM\)
Mà ED//BC (Cma); \(M\in BC\left(gt\right)\)=> ED//CM
Từ 2 chứng minh trên => DEMC là hbh
=>CD//EM(1)
*Mặt khác, ta có: DF//CE(cmb); DF=CE(cmb)
DF//BP(cmc); DF=BP(cmc)
=> CE//BP(cùng //DF); CE=BP(cùng = DF)
Từ chứng minh trên => CEBP là hbh
Nên 2 đường chéo PE và CB cắt nhau tại trung điểm mỗi đường
Mà M là trung điểm CB (gt) => M cũng là trung điểm PE
hay P,M,E thẳng hàng(2)
Từ (1),(2) CD//EP
=> CDEP là hình thang
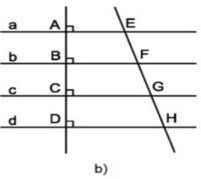
a) Các đường thẳng a, b, c, d song song cách đều ⇒ AB = BC = CD
⇒ B là trung điểm của AC; C là trung điểm của BD
- Hình thang AEGC (AE // GC) có B là trung điểm của AC và BF song song hai cạnh đáy
⇒ F là trung điểm EG (định lí đường trung bình của hình thang)
⇒ EF = FG
- Chứng minh tương tự ⇒ G là trung điểm FH
⇒ FG = GH
Vậy EF = FG = GH