Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) △ABC có : Hai đường cao BE và AD mà 2 đường này cùng cắt nhau tại điểm I ⇒ I là trực tâm
⇒ CI là đường cao còn lại ⇒ CI ⊥ AB
b) Xét △BEC có : góc EBC + gócBEC + góc BCE = \(180^0\)( định lí tổng ba góc )
⇒ góc EBC = \(180^0\) - góc BEC - góc BCE = \(180^0\)- \(90^0\)-\(40^0\)= \(50^0\)
Lại xét △BID có : góc BID + góc IBD + góc BDI = \(180^0\)
⇒ góc BID = \(180^0\) - \(90^0\) - \(50^0\) = \(40^0\)
Có góc BID + góc DIE = \(180^0\)( 2 góc kề bù )
⇒ góc DIE = \(180^0\) - góc BID = \(180^0-40^0\)= \(140^0\)

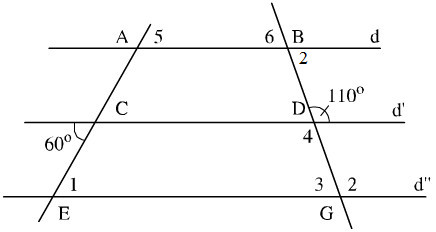
Xem hình vẽ. Có thể tính bằng nhiều cách, chẳng hạn:
+Vì d’ //d’’ có: \(\widehat{E}_1\) và góc 600 là hai góc so le trong nên \(\widehat{E}_1\)= 600
+Vì d’ // d’’ có: \(\widehat{G}_2\)và góc 1100 là hai góc đồng vị nên \(\widehat{G_2}\) = 1100
+ \(\widehat{G}_2\)+\(\widehat{G}_3\)=\(180^0\) (hai góc kề bù)
Nên \(\widehat{G_3}=180^0-\widehat{G}_2=180^0-110^0=70^0\)
+) \(\widehat{D}_4\)1100 (vì là hai góc đối đỉnh)
+) \(\widehat{A}_5\) = \(\widehat{A}_1\) (Hai góc đối đỉnh)
Mà \(\widehat{A}_1\)= 600 (vì là hai góc đồng vị)
Nên \(\widehat{A}_5\) = 600 .
+ \(\widehat{B}_6\) = \(\widehat{B}_2\)(vì là hai góc đối đỉnh)
Mà \(\widehat{B}_2\) + 1100 = 1800 (hai góc trong cùng phía)
Nên \(\widehat{B}_2\) = 1800 - 1100 = 700.
Do đó: \(\widehat{B}_6\) = 700
a) Năm cặp đường thẳng vuông góc là:
d3 ⊥ d4; d3 ⊥ d5; d3 ⊥ d7; d1 ⊥ d8; d1 ⊥ d2
b) Bốn cặp đường thẳng song song là: d4//d5; d5//d7; d4//d7; d8//d2

đây là cậu chép trg chỗ giải đáp rồi mà mk ko đc lm giống trg giải đáp

a) Xét \(\Delta ADE;\Delta BDE:\)
AD = BD (gt)
ED chung
AE = BE (gt)
\(\Rightarrow\Delta ADE=\Delta BDE\left(c.c.c\right)\)
b) Vì \(\Delta ADE=\Delta BDE\) (câu a)
nên \(\widehat{DAE}=\widehat{DBE}\) (2 góc t/ư).
Xem hình vẽ:
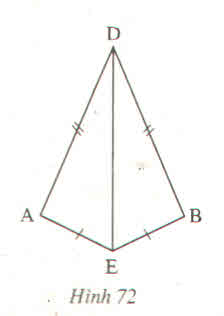
a) ∆ADE và ∆BDE có
DE cạnh chung
AD=DB(gt)
AE=BE(gt)
Vậy ∆ADE=∆BDE(c.c.c)
b) Từ ∆ADE=∆BDE(cmt)
Suy ra \(\widehat{DAE}\)=\(\widehat{DBE}\)(Hai góc tương ứng)
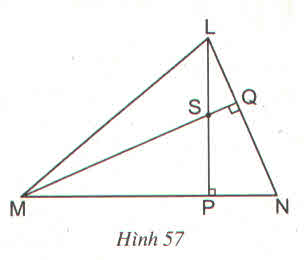







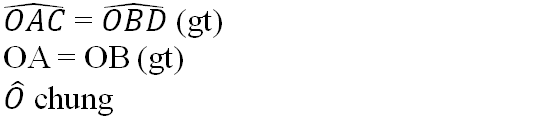



a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)