Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân
a) Các góc của hình thang đều bằng \(90^{\circ}\).
b) Khi \(B C = 6\), chu vi hình thang bằng 24 cm.
a: ABCD là hình thang cân
=>\(\hat{ADC}=\hat{BCD}\)
mà \(\hat{ADC}=2\cdot\hat{BDC}\) (DB là phân giác của góc ADC)
nên \(\hat{BCD}=2\cdot\hat{BDC}\)
Xét ΔBDC vuông tại B có \(\hat{BDC}+\hat{BCD}=90^0\)
=>\(2\cdot\hat{BDC}+\hat{BDC}=90^0\)
=>\(3\cdot\hat{BDC}=90^0\)
=>\(\hat{BDC}=\frac{90^0}{3}=30^0\)
\(\hat{ADC}=2\cdot\hat{BDC}=2\cdot30^0=60^0\)
ABCD là hình thang cân
=>\(\hat{ADC}=\hat{BCD}\)
=>\(\hat{BCD}=60^0\)
AB//CD
=>\(\hat{BAD}+\hat{ADC}=180^0\)
=>\(\hat{BAD}=180^0-60^0=120^0\)
ABCD là hình thang cân
=>\(\hat{BAD}=\hat{ABC}\)
=>\(\hat{ABC}=120^0\)
b: Ta có: AB//CD
=>\(\hat{ABD}=\hat{BDC}\) (hai góc so le trong)
mà \(\hat{ADB}=\hat{BDC}\)
nên \(\hat{ABD}=\hat{ADB}\)
=>AB=AD
mà AD=BC(ABCD là hình thang cân)
nên AB=AD=BC=6(cm)
Xét ΔBCD vuông tại B có \(\sin CDB=\frac{CB}{CD}\)
=>\(\frac{6}{CD}=\sin30=\frac12\)
=>\(CD=2\cdot6=12\left(\operatorname{cm}\right)\)
Chu vi hình thang ABCD là:
AB+BC+CD+DA
=6+6+6+12=18+12=30(cm)
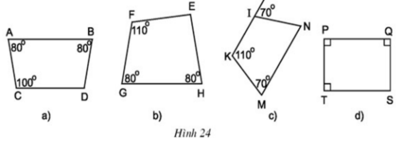
a) Các hình thang cân là : ABDC, IKMN, PQST
b) Áp dụng định lí tổng các góc của một tứ giác bằng 3600
⇒ góc D = 360o- 80o- 80o- 100o = 100o
Góc N = 70o(so le trong với góc 70o)
Góc S = 360o- 90o- 90o- 90o = 90o
c) Hai góc đối của hình thang cân bù nhau