Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

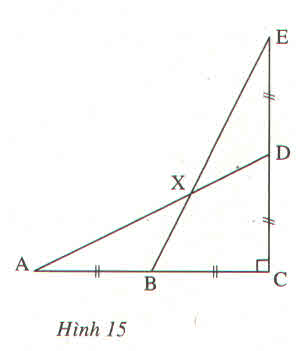
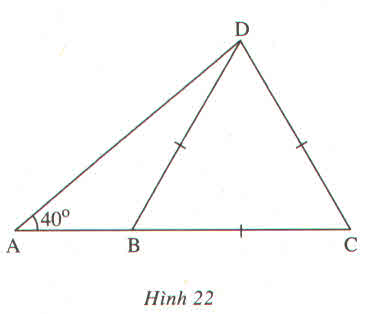
b: XétΔADE vuông tại E có \(AE=AD\cdot\cos A\)
nên AE=5,16(cm)
AB=AE-BE=2,66(cm)

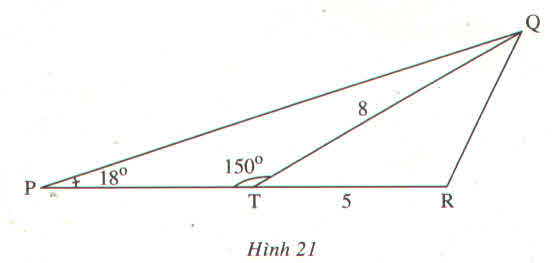
Kẻ QS⊥PR
Ta có : \(\widehat{QTS}=180^0-\widehat{QTP}=180^0-150^0=30^0\)
Trong tam giác vuông QST, ta có:
\(QS=QT.sinQTS=8.sin30^0=4\left(cm\right)\)
\(TS=QT.cosQTS=8.cos30^0\sim6,928\left(cm\right)\)
Trong tam giác vuông QSP, ta có:
\(SP=QS.cotQPS=4.cot18^0=12,311\left(cm\right)\)
\(PT=SP-TS\sim12,311-6,928\sim5,383\left(cm\right)\)
b) Ta có:
\(S_{QPR}=\frac{1}{2}.QS.PR=\frac{1}{2}.QS.\left(PT+TR\right)\sim\frac{1}{2}.4.\left(5,383+5\right)\sim20,766\left(cm^2\right)\)

a: \(x=63\cdot\cos47^0\simeq42,966\left(cm\right)\)
b: \(16=x\cdot\cos38^0\)
nên \(x\simeq20,304\left(cm\right)\)

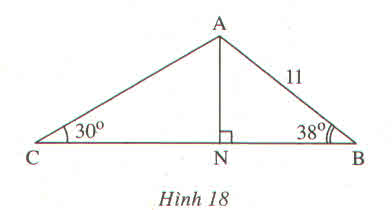
Xét ΔANB vuông tại N có
\(AN=AB\cdot\sin B\)
nên \(AN\simeq6,772\left(cm\right)\)
XétΔACN vuông tại N có
\(AC=\dfrac{AN}{\sin C}=13,544\left(cm\right)\)

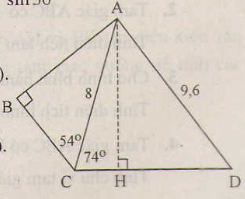
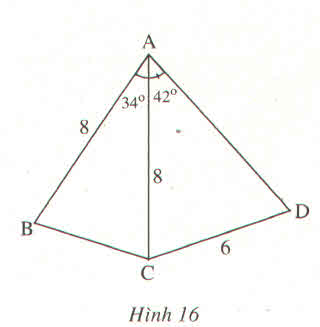
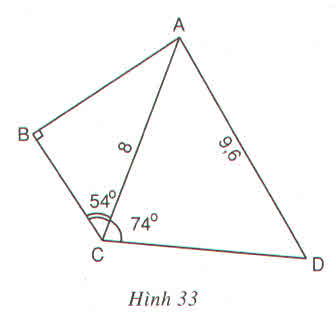
a) Xét tam giác ABC vuông tại B có: AB=AC.sinC=8.sin540≈6,472(cm)AB=AC.sinC=8.sin540≈6,472(cm)
b) Vẽ CD. Xét tam giác ACH có: AH=AC.sinC=8.sin740≈7,690(cm)AH=AC.sinC=8.sin740≈7,690(cm)
Xét tam giác AHD vuông tại H có: sinD=AHAD≈7,6909,6≈0,8010⇒ˆD=530sinD=AHAD≈7,6909,6≈0,8010⇒D^=530
Nhận xét: Để tính được số đo của góc D, ta đã vẽ AH ⊥ CD. Mục đích của việc vẽ đường phụ này là để tạo ra tam giác vuông biết độ dài hai cạnh và có góc D là một góc nhọn của nó. Từ đó tính được một tỉ số lượng giác của góc D rồi suy ra số đo của góc D.