Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thấy kính này phải là thấu kính hội tụ, vì thấu kính phân kì thì đặt vật ở đâu cũng thỏa mãn.
Trong thấu kính hội tụ, nếu đặt vật cách thấu kính là d > f thì vật thật luôn cho ảnh thật ngược chiều với vật.
Ta có: Vật AB
AB ----TK ----> A1B1
AB----Gương---->A'B'----->TK----->A2B2
Do A'B' nằm trong gương nên cách thấu kính là d > 2f, vì vậy ảnh A2B2 là ảnh thật ngược chiều với A'B', cũng ngược chiều với AB.
Do đó, A1B1 cũng phải ngược chiều với AB.
Suy ra, vật AB đặt trong khoảng d sau cho: f<d<2f

Bài này bn cần xét 2 TH và tìm mối quan hệ của các đại lượng chưa bt vs đại lượng đã bt( chủ yếu sd tam giác đồng dạng). Mk dùng mt nên lười vẽ hình và tb, thông cảm, bn cứ lm theo mk bảo, sẽ ra thôi, phần này là phần cơ bản nên rất dễ, nếu có j thắc mắc cứ hỏi :))

Tham khảo:
Ảnh thật, ngược chiều, lớn hơn vật và cách thấu kính một khoảng 60cm.
Lời giải: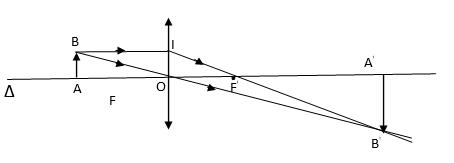
giải tính chiều cao:
ΔOAB ∼ ΔOA'B'
=> \(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\left(1\right)\)
ta lại có :
Δ OIF ∼ Δ A'B'F'
=> \(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'B'}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}\left(3\right)\)
mà : A'F' = OA' - OF ' (4)
thay số vào (3) và (4) ta được : OA' = 60cm

a/ Đổi 0,1mm2 = 1. 10-7 m2 . Áp dụng công thức tính điện trở \(R=\rho\frac{l}{S}\) ; thay số và tính \(\Rightarrow\) RAB = 6W
b/ Khi \(AC=\frac{BC}{2}\) \(\Rightarrow\) RAC = \(\frac{1}{3}\).RAB Þ RAC = 2W và có RCB = RAB - RAC = 4W
Xét mạch cầu MN ta có \(\frac{R_1}{R_{AC}}=\frac{R_2}{R_{CB}}=\frac{3}{2}\) nên mạch cầu là cân bằng. Vậy IA = 0
c/ Đặt RAC = x ( ĐK : \(0\le x\le6\Omega\) ) ta có RCB = ( 6 - x )
* Điện trở mạch ngoài gồm ( R1 // RAC ) nối tiếp ( R2 // RCB ) là \(R=\frac{3.x}{3+x}+\frac{6.\left(6-x\right)}{6+\left(6-x\right)}=\)= ?
* Cường độ dòng điện trong mạch chính : \(I=\frac{U}{R}\) ?
* Áp dụng công thức tính HĐT của mạch // có : UAD = RAD . I = \(\frac{3.x}{3+x}.I=\) ?
Và UDB = RDB . I = \(\frac{6.\left(6-x\right)}{12-x}I\) = ?
* Ta có cường độ dòng điện qua R1 ; R2 lần lượt là : I1 = \(\frac{U_{AD}}{R_1}\) = ? và I2 = \(\frac{U_{DB}}{R_2}\) = ?
+ Nếu cực dương của ampe kế gắn vào D thì : I1 = Ia + I2 Þ Ia = I1 - I2 = ? (1)
Thay Ia = 1/3A vào (1) Þ Phương trình bậc 2 theo x, giải PT này được x = 3W ( loại giá trị -18)
+ Nếu cực dương của ampe kế gắn vào C thì : Ia = I2 - I1 = ? (2)
Thay Ia = 1/3A vào (2) Þ Phương trình bậc 2 khác theo x, giải PT này được x = 1,2W ( loại 25,8 vì > 6 )
* Để định vị trí điểm C ta lập tỉ số \(\frac{AC}{CB}=\frac{R_{AC}}{R_{CB}}\) = ? \(\Rightarrow\) AC = 0,3m
