Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: D = m − 1 3 m = m 2 + 3 ; D x = 2 − 1 5 m = 2 m + 5 ; D y = m 2 3 5 = 5 m − 6
Vì m 2 + 3 ≠ 0 , ∀ m nên hệ phương trình luôn có nghiệm duy nhất x = D x D = 2 m + 5 m 2 + 3 y = D y D = 5 m − 6 m 2 + 3
Theo giả thiết, ta có:
x + y < 1 ⇔ 2 m + 5 m 2 + 3 + 5 m − 6 m 2 + 3 < 1 ⇔ 7 m − 1 m 2 + 3 < 1
⇔ 7 m − 1 < m 2 + 3 ⇔ m 2 − 7 m + 4 > 0 ⇔ m > 7 + 33 2 m < 7 − 33 2
Đáp án cần chọn là: A

Ta có:
D = m − 2 3 m = m 2 + 6 ; D x = 3 − 2 4 m = 3 m + 8 ; D y = m 3 3 4 = 4 m − 9
Vì m 2 + 6 ≠ 0 , ∀ m nên hệ phương trình luôn có nghiệm duy nhất x = D x D = 3 m + 8 m 2 + 6 y = D y D = 4 m − 9 m 2 + 6
Theo giả thiết, ta có:
x > 0 y < 0 ⇔ 3 m + 8 m 2 + 6 > 0 4 m − 9 m 2 + 6 < 0 ⇔ 3 m + 8 > 0 4 m − 9 < 0 ⇔ m > − 8 3 m < 9 4
⇔ − 8 3 < m < 9 4
Vì m ∈ Z nên m ∈ {−2; −1; 0; 1; 2}
Đáp án cần chọn là: B

Ta có: D = m m + 2 1 m = m 2 − m − 2
D x = 5 m + 2 2 m + 3 m = 5 m − ( m + 2 ) ( 2 m + 3 ) = − 2 m 2 − 2 m − 6
D y = m 5 1 2 m + 3 = 2 m 2 + 3 m − 5
Để hệ phương trình có nghiệm duy nhất thì D ≠ 0 ⇔ m 2 − m − 2 ≠ 0 ⇔ m ≠ − 1 m ≠ 2
Khi đó: x = D x D = − 2 ( m 2 + m + 3 ) m 2 − m − 2 ; y = D y D = 2 m 2 + 3 m − 5 m 2 − m − 2
Để hệ phương trình có nghiệm âm thì: − 2 ( m 2 + m + 3 ) m 2 − m − 2 < 0 ( 1 ) 2 m 2 + 3 m − 5 m 2 − m − 2 < 0 ( 2 )
1 ⇔ m 2 + m + 3 m 2 − m − 2 > 0 ⇔ m 2 − m − 2 > 0 ( v ì m 2 + m + 3 = m + 1 2 2 + 11 4 > 0 , ∀ m )
⇔ m < − 1 m > 2 *
2 ⇔ 2 m 2 + 3 m − 5 > 0 m 2 − m − 2 < 0 2 m 2 + 3 m − 5 < 0 m 2 − m − 2 > 0 ⇔ m < − 5 2 m > 1 − 1 < m < 2 − 5 2 < m < 1...

\(\hept{\begin{cases}mx+y=m^2+m+1\\-x+my=m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}m\left(my-m^2\right)+y-m^2-m-1=0\\x=my-m^2\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}\left(m^2y-m^2\right)+\left(y-1\right)-\left(m^3+m\right)=0\\x=my-m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(m^2+1\right)\left(y-m-1\right)=0\\x=my-m^2\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}y=m+1\\x=m\left(m+1\right)-m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=m\\y=m+1\end{cases}}\)
\(\Rightarrow\)\(x^2+y^2=2m^2+2m+1=2\left(m+\frac{1}{2}\right)^2+\frac{1}{2}\ge\frac{1}{2}\)
Dấu "=" xảy ra khi \(m=\frac{-1}{2}\) hay hệ có nghiệm \(\left(x;y\right)=\left(\frac{-1}{2};\frac{1}{2}\right)\)

Ta có D = m − 1 2 m = m 2 + 2 > 0 , ∀ m ∈ R nên hệ phương trình luôn có nghiệm duy nhất
D x = 3 − 1 9 m = 3 m + 9 ; D y = m 3 2 9 = 9 m − 6
Vậy hệ luôn có nghiệm duy nhất là: x = 3 m + 9 m 2 + 2 y = 9 m − 6 m 2 + 2
Ta có: A = 3 x − y = 3 3 m + 9 m 2 + 2 − 9 m − 6 m 2 + 2 = 33 m 2 + 2
Vì m ∈ Z nên để A nguyên thì m 2 + 2 là ước của 33 mà m 2 + 2 ≥ 2 nên ta có các trường hợp sau:

Mà m nguyên dương nên m ∈ 1 ; 3
Vậy có 2 giá trị nguyên dương của m để A nguyên.
Đáp án cần chọn là: B

1.
\(\left\{{}\begin{matrix}\left(x^2-2x\right)\left(y^2-6y\right)=m\\\left(x^2-2x\right)+\left(y^2-6y\right)=3m\end{matrix}\right.\)
Theo Viet đảo, \(x^2-2x\ge-1\) và \(y^2-6y\ge-9\) là nghiệm của:
\(t^2-3m.t+m=0\) (1)
Hệ đã cho có đúng 3 nghiệm khi và chỉ khi:
TH1: (1) có 1 nghiệm \(t_1=-1\) và 1 nghiệm \(t_2>-9\)
\(t=-1\Rightarrow1+3m+m=0\Rightarrow m=-\dfrac{1}{4}\)
\(\Rightarrow t_2=\dfrac{1}{4}\) (thỏa mãn)
TH2: (1) có 1 nghiệm \(t_1=-9\) và 1 nghiệm \(t_2>-1\)
\(t_1=-9\Rightarrow81+27m+m=0\Leftrightarrow m=-\dfrac{81}{28}\)
\(\Rightarrow t_2=\dfrac{9}{28}\) (thỏa mãn)
Vậy \(m=\left\{-\dfrac{1}{4};-\dfrac{81}{28}\right\}\)
2. Pt bậc 2 có nghiệm duy nhất thì nó là nghiệm kép
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(m+3\right)^2-4\left(2m-1\right)=0\left(vô-nghiệm\right)\\\dfrac{m+3}{2}\le3\end{matrix}\right.\)
Ko tồn tại m thỏa mãn
Hoặc là ngôn ngữ đề bài có vấn đề, ý của người ra đề là "phương trình đã cho có 2 nghiệm, trong đó có đúng 1 nghiệm thỏa mãn \(x\le3\)"?

Hệ: m x + 3 m − 2 y + m − 3 = 0 2 x + m + 1 y − 4 = 0 ⇔ m x + 3 m − 2 y = 3 − m 2 x + m + 1 y = 4
Ta có:
D = m 3 m − 2 2 m + 1 = m 2 − 5 m + 4 = m − 1 m − 4
D x = 3 − m 3 m − 2 4 m + 1
= 3 − m m + 1 − 4 3 m − 2 = − m + 11 = 1 − m m + 11
D y = m 3 − m 2 4 = 4 m − 6 + 2 m = 6 m − 6 = 6 m − 1
Hệ phương trình có nghiệm duy nhất
⇔ D ≠ 0 ⇔ m − 1 m − 4 ≠ 0 ⇔ m ≠ 1 m ≠ 4
⇒ x = D x D = 1 − m m + 11 m − 1 m − 4 = m + 11 4 − m ( 1 ) y = D y D = 6 m − 1 m − 1 m − 4 = 6 m − 4 ( 2 )
Từ 2 ⇒ m − 4 y = 6 ⇔ m y = 6 + 4 y ⇔ m = 6 + 4 y y = 6 y + 4
Thay vào (1) ta được:
x = 6 y + 4 + 11 : 4 − 6 y − 4 = − 6 + 15 y 6 = − 1 − 15 6 y
Đáp án cần chọn là: C
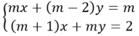
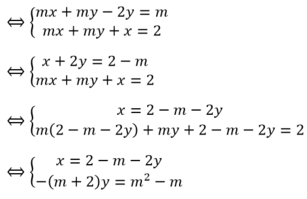
Hệ pt : \(\begin{cases}x+my=m+1\\mx+y=3m-1\end{cases}\)
Xét pt đầu : \(x+my=m+1\Leftrightarrow x=m+1-my\) thay vào pt còn lại :
\(m\left(m+1-my\right)+y=3m-1\)
\(\Leftrightarrow y\left(1-m^2\right)=-m^2+2m-1\)
Nếu \(m=1\) thì pt có dạng 0.y = 0 => Vô số nghiệm.
Nếu m = -1 thì pt có dạng 0.x = -4 => vô nghiệm.
Xét với \(m\ne1\) và \(m\ne-1\) thì pt có nghiệm \(y=\frac{-\left(m-1\right)^2}{\left(1-m\right)\left(1+m\right)}=\frac{m-1}{m+1}\)
\(\Rightarrow x=m+1-m\left(\frac{m-1}{m+1}\right)=m+1-\frac{m^2-m}{m+1}=\frac{m^2+2m+1-m^2+m}{m+1}=\frac{3m+1}{m+1}\)
Xét \(xy=\frac{\left(m-1\right)\left(3m+1\right)}{\left(m+1\right)^2}=\frac{3m^2-2m-1}{\left(m+1\right)^2}\)
Đặt \(t=m+1\) thì \(m=t-1\) thay vào biểu thức trên được
\(\frac{3\left(t-1\right)^2-2\left(t-1\right)-1}{t^2}=\frac{3t^2-8t+4}{t^2}=\frac{4}{t^2}-\frac{8}{t}+3\)
Lại đặt \(a=\frac{1}{t}\) thì : \(4a^2-8a+3=4\left(a-1\right)^2-1\ge-1\)
Suy ra \(xy\ge-1\) . Dấu đẳng thức xảy ra khi \(a=1\Leftrightarrow t=1\Leftrightarrow m=0\)
Vậy với m = 0 thì xy đạt giá trị nhỏ nhất bằng -1
cam on