Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(det=\left|\begin{matrix}1&-m\\m&1\end{matrix}\right|=1+m^2\ne0\) với mọi m => Hệ phương trình bậc nhất hai ẩn luôn có nghiệm
b) Ta có:
x0 - my0 = 2 - 4m
mx0 + y0 = 3m + 1
Hay là:
x0 - 2 = m (y0 - 4)
y0 - 1 = m (3 - x0)
=> Chia hai vế cho nhau ta được
\(\frac{x_0-2}{y_0-1}=\frac{y_0-4}{3-x_0}\)
=> (x0 - 2)(3 - x0) = (y0 - 4)(y0 - 1)
=> -x02 + 5x0 - 6 = y02 - 5y0 + 4
=> x02 + y02 - 5(x0 + y0) = -10
ĐPCM

a) Cả hai phương trình đều có chung \(\sqrt{x+3}\)
pt đầu suy ra \(\sqrt{x+3}=2\sqrt{y-1}\)
pt sau suy ra \(\sqrt{x+3}=4-\sqrt{y+1}\)
Vậy \(2\sqrt{y-1}=4-\sqrt{y+1}\), đk y > 1
\(4\left(y-1\right)=16-8\sqrt{y+1}+y+1\)
\(8\sqrt{y+1}+3y-21=0\)
Đặt \(\sqrt{y+1}=t\)
=> y = t2 - 1
=> 8t + 3(t2 -1) -21 =0
3t2 + 8t - 24 = 0
=> t = ...
=> y = t2 - 1
=> \(\sqrt{x+3}=2\sqrt{y-1}\)
=> x =...
b) Trừ hai pt cho nhau ta có:
x2 - y2 = 3(y - x)
(x - y) (x + y + 3) = 0
=> x = y hoặc x + y + 3 = 0
Xét hai trường hợp, rút x theo y rồi thay trở lại một trong hai pt ban đầu tìm ra nghiệm
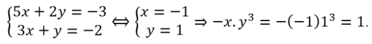
Đáp án: D