Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

pt có 2 nghiệm pb dương
<=> {delta=25-4m>0
{ x1+x2=5>0
{x1..x2=m>0
<=> 0<m <25/4
( x1canx2+x2canx1)2=36
x1^2..x2 +x1 ..x2^2 +2 (x1×x2)can (x1×x2)=36
sau đó sử ddụng viet và thay vào
mn cho mk hỏi
nếu đđặt câu hỏi trên OLM này thì khi có người giải đáp cho mk thì có thông báo k z
Lập \(\Delta=25-4m\)
Phương trình có 2 nghiệm \(x_1;x_2\)khi \(\Delta\ge0\)hay \(m\le\frac{25}{4}\)
Áp dụng hệ thức Vi-et ta có \(\hept{\begin{cases}x_1+x_2=5\\x_1x_2=m\end{cases}}\)
2 nghiệm \(x_1;x_2\)dương khi \(\hept{\begin{cases}x_1+x_2>0\\x_1x_2>0\end{cases}}\)hay m>0
Điều kiện để pt có 2 nghiệm dương x1;x2 là \(0< m< \frac{25}{4}\)(*)
Ta có \(\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=x_1+x_2+2\sqrt{x_1x_2}=5+2\sqrt{m}\)
=> \(\sqrt{x_1}+\sqrt{x_2}=\sqrt{5+2\sqrt{m}}\)
Ta có \(x_1\sqrt{x_2}+x_2\sqrt{x_1}=6\Leftrightarrow\sqrt{x_1x_2}\left(\sqrt{x_1}+\sqrt{x_2}\right)=6\)
hay \(\sqrt{m}\sqrt{5+2\sqrt{m}}=6\Leftrightarrow2m\sqrt{m}+5m-36=0\left(1\right)\)
Đặt \(t=\sqrt{m}\ge0\)khi đó (1) trở thành
\(\Leftrightarrow2t^2+5t^2-36=0\)
\(\Leftrightarrow\left(t-2\right)\left(2t^2+9t+18\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t-2=0\\2t^2+9t+18=0\end{cases}\Rightarrow t=2\Rightarrow m=4\left(tmđk\right)}\)
(vì 2t2+9t+18 vô nghiệm)
Vậy m=4 thì pt đã cho có 2 nghiệm dương x1;x2 thỏa mãn \(x_1\sqrt{x_2}+x_2\sqrt{x_1}=6\)

\(\Delta'=1-\left(2m-1\right)=2-2m\ge0\Rightarrow m\le1\)
Để biểu thức đề bài xác định thì pt có 2 nghiệm dương
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2>0\\x_1x_2=2m-1>0\end{matrix}\right.\) \(\Rightarrow m>\frac{1}{2}\)
\(\frac{1}{\sqrt{x_1}}+\frac{1}{\sqrt{x_2}}=2\Leftrightarrow\sqrt{x_1}+\sqrt{x_2}=2\sqrt{x_1x_2}\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=4x_1x_2\)
\(\Leftrightarrow2+2\sqrt{2m-1}=4\left(2m-1\right)\)
\(\Leftrightarrow2\left(2m-1\right)-\sqrt{2m-1}-1=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{2m-1}=1\\\sqrt{2m-1}=-\frac{1}{2}\left(l\right)\end{matrix}\right.\) \(\Rightarrow m=1\) (thỏa mãn)

Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=\frac{b}{a}=\frac{ab}{a^2}>0\\x_1x_2=\frac{b}{a}=\frac{ab}{a^2}>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1>0\\x_2>0\end{matrix}\right.\)
\(\sqrt{\frac{x_1}{x_2}}+\sqrt{\frac{x_2}{x_1}}-\sqrt{\frac{b}{a}}=\frac{x_1+x_2}{\sqrt{x_1x_2}}-\sqrt{\frac{b}{a}}=\frac{\frac{b}{a}}{\sqrt{\frac{b}{a}}}-\sqrt{\frac{b}{a}}=\sqrt{\frac{b}{a}}-\sqrt{\frac{b}{a}}=0\)

ta thấy pt luôn có no . Theo hệ thức Vi - ét ta có:
x1 + x2 = \(\dfrac{-b}{a}\) = 6
x1x2 = \(\dfrac{c}{a}\) = 1
a) Đặt A = x1\(\sqrt{x_1}\) + x2\(\sqrt{x_2}\) = \(\sqrt{x_1x_2}\)( \(\sqrt{x_1}\) + \(\sqrt{x_2}\) )
=> A2 = x1x2(x1 + 2\(\sqrt{x_1x_2}\) + x2)
=> A2 = 1(6 + 2) = 8
=> A = 2\(\sqrt{3}\)
b) bạn sai đề

Cô hướng dẫn thôi nhé ^^
Coi phương trình trên là phương trình bậc hai với ẩn \(\sqrt{x}\)
Để phương trình trên có 2 nghiệm \(x_1;x_2\) thì nó phải có 2 nghiệm phân biệt cùng dương \(\sqrt{x _1};\sqrt{x_2}\).
Điều này tương đương \(\Delta>0,S>0,P>0\) hay \(\frac{9}{4}>m>\frac{3}{2}\)
Khi đó theo Viet ta có: \(\sqrt{x_1}+\sqrt{x_2}=\sqrt{6}\); \(\sqrt{x_1x_2}=2m-3\)
Vậy điều kiện trên tương đương: \(\frac{\left(\sqrt{x_1}+\sqrt{x_2}\right)^2-2\sqrt{x_1x_2}}{\sqrt{x_1}+\sqrt{x_2}}=\frac{\sqrt{24}}{3}\)
Thế vào ta có: \(\frac{6-2\left(2m-3\right)}{\sqrt{6}}=\frac{\sqrt{24}}{3}\Rightarrow12-4m=4\Rightarrow m=2\)
Chúc em học tốt ^^

a) Phương trình \(x^2-2mx-2m-1=0\)có các hệ số a = 1; b = - 2m; c = - 2m - 1
\(\Delta=\left(-2m\right)^2-4\left(-2m-1\right)=4m^2+8m+4=4\left(m+1\right)^2\ge0\forall m\)
Vậy phương trình luôn có 2 nghiệm x1, x2 với mọi m (đpcm)
b) Theo Viète, ta có: \(x_1+x_2=2m;x_1x_2=-2m-1\)
Hệ thức \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{-5}{2}\Leftrightarrow2\left(x_1^2+x_2^2\right)=-5x_1x_2\)
\(\Leftrightarrow2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=-5x_1x_2\)hay \(2\left(4m^2+4m+2\right)=10m+5\Leftrightarrow8m^2-2m-1=0\)\(\Leftrightarrow\orbr{\begin{cases}m=\frac{1}{2}\\m=-\frac{1}{4}\end{cases}}\)
Vậy \(m=\frac{1}{2}\)hoặc \(m=-\frac{1}{4}\)thì phương trình có 2 nghiệm x1, x2 thỏa mãn\(\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{-5}{2}\)
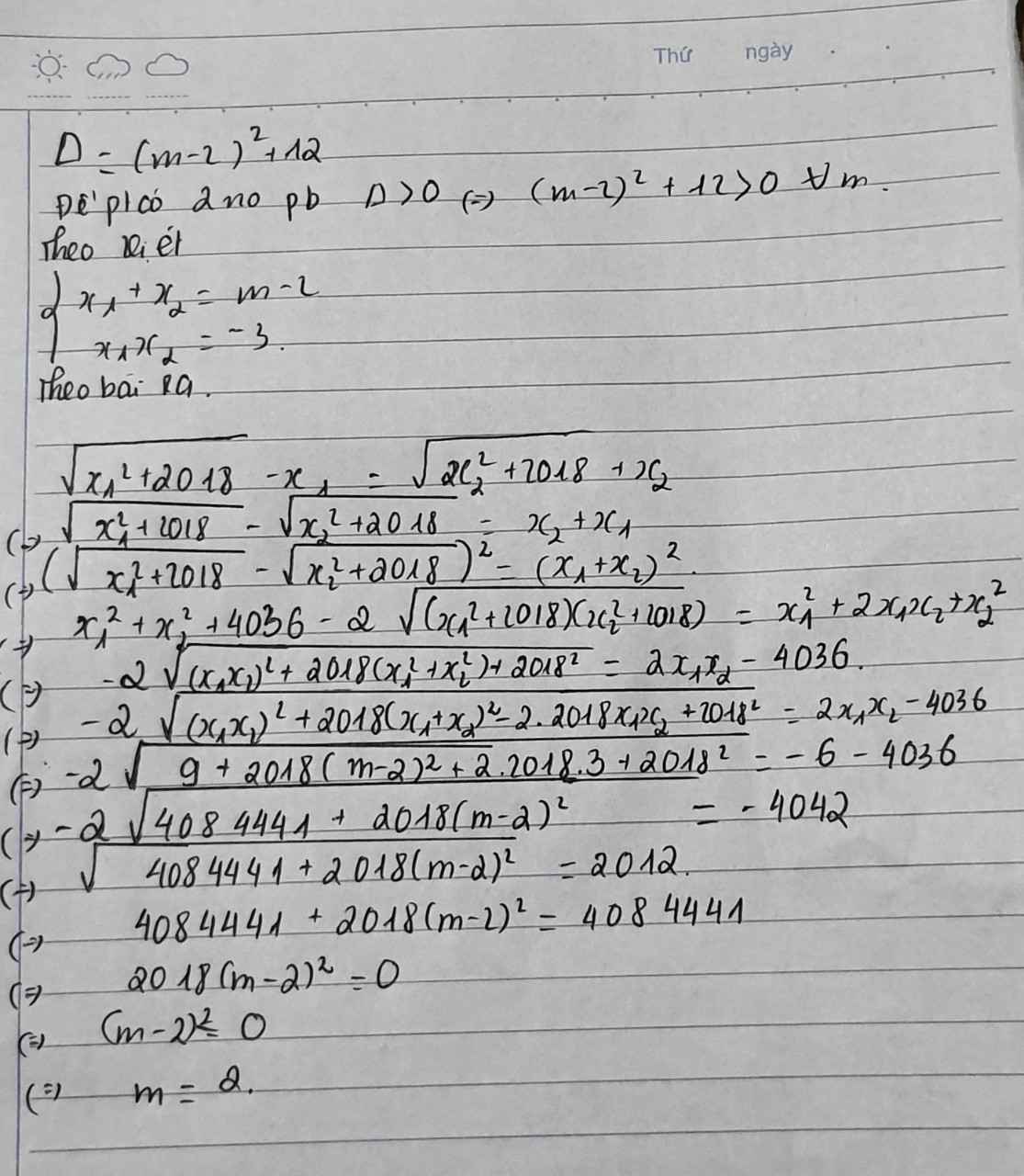
Đặt \(t=\sqrt{x}\left(t\ge0\right)\Rightarrow t^2-\sqrt{6}t-3+2m=0\left(1\right)\)
Giả sử phương trình $(1)$ có nghiệm $t_1;t_2$ thì \(t_1+t_2=\sqrt{6}\) và \(t_1.t_2=2m-3\)
\(t_1=\sqrt{x_1}\left(t_1\ge0\right)\Rightarrow x_1=t_1^2\) và \(t_2=\sqrt{x_2}\left(t_2\ge0\right)\Rightarrow x_2=t_2^2\)
Ta có: \(\dfrac{{{x_1} + {x_2}}}{{\sqrt {{x_1}} + \sqrt {{x_2}} }} = \dfrac{{\sqrt {24} }}{3}\)
\(\Leftrightarrow \dfrac{{t_1^2 + t_2^2}}{{{t_1} + {t_2}}} = \dfrac{{\sqrt {24} }}{3}\\ \Leftrightarrow \dfrac{{{{\left( {{t_1} + {t_2}} \right)}^2} - 2{t_1}{t_2}}}{{{t_1} + {t_2}}} = \dfrac{{\sqrt {24} }}{3}\\ \Leftrightarrow \dfrac{{6 + 6 - 4m}}{{\sqrt 6 }} = \dfrac{{\sqrt {24} }}{3} \Leftrightarrow m = 2\left( {tm} \right)\)
thank you very much!!