Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
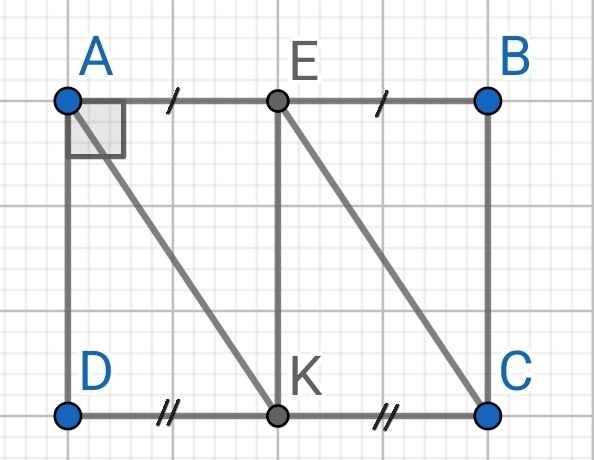a) Do E là trung điểm của AB (gt)
⇒ AE = AB : 2
Do K là trung điểm của CD (gt)
⇒ CK = DK = CD : 2
Mà AB = CD (do ABCD là hình chữ nhật)
⇒ AE = CK
Lại có AB // CD (do ABCD là hình chữ nhật)
⇒ AE // CK
Tứ giác AECK có:
AE // CK (cmt)
AE = CK (cmt)
⇒ AECK là hình bình hành
b) Do AE = AB : 2 (cmt)
DK = CD : 2 (cmt)
AB = CD (cmt)
⇒ AE = DK
Lại có:
AB // CD (cmt)
⇒ AE // DK
Tứ giác AEKD có:
AE // DK (cmt)
AE = DK (cmt)
⇒ AEKD là hình bình hành
Mà ∠EAK = 90⁰ (do ABCD là hình chữ nhật)
⇒ AEKD là hình chữ nhật
⇒ ∠AEK = 90⁰
Hay AE ⊥ EK
a)ta có:
AB=DC mà AE=1/2 AB, KC= 1/2 DC
=>AE=KC
Xét tứ giác AECK, ta có:
AE//KC(AB//KC và AE thuộc AB và KC thuộc DC)
=>tứ giác AECK là hình bình hành.
b) chỗ DE vuông góc CE có đúng không vậy để mai mình làm tiếp
1: E là trung điểm của AB
=>\(EA=EB=\dfrac{AB}{2}\)(1)
K là trung điểm của CD
=>\(DK=KC=\dfrac{DC}{2}\)(2)
ABCD là hình vuông
=>AB=DC(3)
Từ (1),(2),(3) suy ra AE=EB=CK=KD
Xét tứ giác AECK có
AE//CK
AE=CK
Do đó: AECK là hình bình hành
2: Xét ΔFCD vuông tại C và ΔEBC vuông tại B có
FC=EB
CD=BC
Do đó: ΔFCD=ΔEBC
=>\(\widehat{FDC}=\widehat{ECB}\)
mà \(\widehat{FDC}+\widehat{DFC}=90^0\)(ΔDFC vuông tại C)
nên \(\widehat{ECB}+\widehat{DFC}=90^0\)
=>DF\(\perp\)CE tại M
3: AECK là hình bình hành
=>AK//CE
AK//CE
CE\(\perp\)DF
Do đó: AK\(\perp\)CE tại N
Xét ΔDMC có
K là trung điểm của DC
KN//MC
Do đó: N là trung điểm của DM
4: Xét ΔADM có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔADM cân tại A
=>AD=AM
mà AD=AB
nên AM=AB
Sửa đề: F là hình chiếu của E trên AC
a: Xét ΔCAB có
E là trung điểm của CB
EF//AB
=>F là trung điểm của AC
Xét ΔCAB có
E là trung điểm của CB
ED//AC
=>D là trung điểm của AB
Xét ΔABC có EF//AB
nên EF/Ab=CE/CB=1/2
=>EF=1/2AB=DB
Xét tứ giác BDFE có
FE//BD
FE=BD
=>BDFE là hình bình hành
b: Xét ΔABC có AD/AB=AF/AC
nên DF//BC
=>DF//EH
ΔHAC vuông tại H có HF là trung tuyến
nên HF=AC/2
=>HF=ED
Xét tứ giác EHDF có
EH//DF
ED=HF
=>EHDF là hình thang cân
c: Xét tứ giác ABCN có
F là trung điểm chung của AC và BN
=>ABCN là hình bình hành
=>AN//CB
Xét tứ giác AMCE có
F là trung điểm chung của AC và ME
=>AMCE là hình bình hành
=>AM//CE
=>AM//CB
mà AN//CB
nên A,N,M thẳng hàng
△HBA đồng dạng △ABC.
1/3 AH.
⇒ AE = AB : 2
Do K là trung điểm của CD (gt)
⇒ CK = DK = CD : 2
Mà AB = CD (do ABCD là hình chữ nhật)
⇒ AE = CK
Lại có AB // CD (do ABCD là hình chữ nhật)
⇒ AE // CK
Tứ giác AECK có:
AE // CK (cmt)
AE = CK (cmt)
⇒ AECK là hình bình hành
b) Do AE = AB : 2 (cmt)
DK = CD : 2 (cmt)
AB = CD (cmt)
⇒ AE = DK
Lại có:
AB // CD (cmt)
⇒ AE // DK
Tứ giác AEKD có:
AE // DK (cmt)
AE = DK (cmt)
⇒ AEKD là hình bình hành
Mà ∠EAK = 90⁰ (do ABCD là hình chữ nhật)
⇒ AEKD là hình chữ nhật
⇒ ∠AEK = 90⁰
Hay AE ⊥ EK