Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

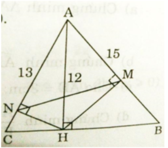
a) Xét ΔANH và ΔAHC có:
∠(NAH) chung
∠(ANH) = ∠(AHN) = 90o
⇒ ΔANH ∼ ΔAHC (g.g)
b) Ta có :
![]()
![]()
Tương tự : CH = 5 (cm)
⇒ BC = BH + CH = 9 + 5 = 14 (cm)
c) Theo chứng minh trên ta có:
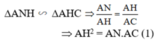
Chứng minh tương tự ta có :
ΔAMH ∼ ΔAHB ⇒ AH2 = AM.AB (2)
Từ (1) và (2) ⇒ AN.AC = AM.AB (3)
Xét ΔAMN và ΔACB có :
∠A chung
AN.AC = AM.AB
⇒ ΔAMN ∼ ΔACB (c.g.c)
d) Ta có : ΔAMH ∼ ΔAHB
![]()
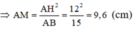
Lại có ΔAMN ∼ ΔACB (cmt)
![]()
![]()

a,b bạn làm r nên mình k làm lại
c) ở câu b) ta đã c/m được P là trực tâm của tam giác AMD nên DP vuông góc với AM (1)
Mà MNDP là hình bình hành (câu a)) => DP // MN (2)
Từ (1) và (2) suy ra đpcm
haizzz, sao k đăng một lần luôn :|
Từ N kẻ NH vuông góc với AC tại H
Dễ thấy HN là đường tb của tam giác ODC nên HO = OC => H là trung điểm của OC
Do đó AH = MD
Xét tam giác vuông AHN có AN là cạnh huyền
=> AN > AH = MD

a: Xét ΔHDC có
N là trung điểm của HD
M là trung điểm của HC
Do đó: NM là đường trung bình của ΔHDC
Suy ra: NM//DC và \(NM=\dfrac{CD}{2}\)
mà AB//DC và \(AB=\dfrac{CD}{2}\)
nên NM//AB và NM=AB
b: Xét tứ giác ABMN có
AB//NM
AB=NM
Do đó: ABMN là hình bình hành

A ) ÁP DỤNG ĐỊNH LÍ PITAGO TA CÓ :
\(BH^2=AB^2-AH^2\)
\(\Leftrightarrow\)\(15^2-12^2=81\)
\(\Rightarrow BH=\sqrt{81}=9\)(cm)
Ap dụng pitago ta lại có :
\(HC^2=AC^2-AH^2\)
\(\Leftrightarrow HC^2=13^2-12^2=25\left(CM\right)\)
\(\Rightarrow HC=\sqrt{25}=5\left(cm\right)\)
Vậy : \(BC=BH+HC=5+9=14\left(cm\right)\)
sao lại sử dụng Py - ta - go đc ? tam giác ABC nhọn mà



