Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(u\left(1\right)=1^2=1\\ u\left(2\right)=2^2=4\\ u\left(50\right)=50^2=2500\\ u\left(100\right)=100^2=10000.\)
u(1)=1^2=1
u(2)=2^2=4
u(50)=50^2=2500
u(100)=100^2=10000

a)
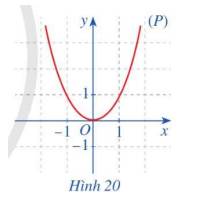
Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2},f\left( x \right) = {x^2} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)
Trục đối xứng của (P) là đường thẳng y = 0
b)
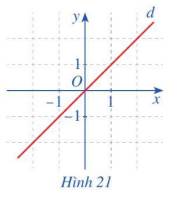
Ta có: \(g\left( { - x} \right) = - g\left( x \right)\)
Gốc tọa độ O là tâm đối xứng của đường thẳng d

[cos (3x + π/2) + 1] . sin (x + π/5) = 0 (*)
<=> cos (3x + π/2) + 1 = 0 hoặc sin (x + π/5) = 0
<=> cos (3x + π/2) = -1 hoặc sin (x + π/5) = 0
<=> 3x + π/2 = π + k2 π hoặc x + π/5 = k π (k∈Z)
<=> x = π/6 + k2 π/3 hoặc x = - π/5 + k π (k∈Z)
Vậy phương trình (*) có các họ nghiệm …

Đường tròn \(\left(C_1\right)\) tâm \(A\left(-1;1\right)\) bán kính \(R=3\)
Đường tròn \(\left(C_2\right)\) tâm \(B\left(3;-2a\right)\) bán kính \(R'=\sqrt{3a^2-a+5}\)
Do \(\left(C_2\right)\) là ảnh của \(\left(C_2\right)\) qua phép tịnh tiến nên \(R=R'\)
\(\Leftrightarrow3a^2-a+5=9\Leftrightarrow3a^2-a-4=0\Rightarrow\left[{}\begin{matrix}a=-1\\a=\frac{4}{3}\notin Z\left(l\right)\end{matrix}\right.\)
\(\Rightarrow B\left(3;2\right)\)
\(\Rightarrow\overrightarrow{v}=\overrightarrow{AB}=\left(4;1\right)\)
\(\Rightarrow\) Tổng tung và hoành độ bằng 5

1/ Dễ thấy \(\left(x_n\right)\) là dãy dương
\(\frac{x_{n+1}}{x_n}=\frac{\left(n+2\right)!}{2^{n+1}}.\frac{2^n}{\left(n+1\right)!}=\frac{n+2}{2}=1+\frac{n}{2}>1\)
\(\Rightarrow x_{n+1}>x_n\Rightarrow x_n\) là dãy tăng
Ta có \(0< sin^2\left(n+1\right)< 1\) \(\forall n\in N\) \(\Rightarrow1-sin^2\left(n+1\right)>0\)
\(y_{n+1}-y_n=n+1+sin^2\left(n+2\right)-\left(n+sin^2\left(n+1\right)\right)\)
\(=1-sin^2\left(n+1\right)+sin^2\left(n+2\right)>sin^2\left(n+2\right)>0\)
\(\Rightarrow y_{n+1}>y_n\Rightarrow y_n\) là dãy tăng
2/ \(\left\{{}\begin{matrix}u_1=3\\u_{n+1}=\frac{1}{4}u_n\end{matrix}\right.\) \(\Rightarrow u_n\) là cấp số nhân với công bội \(q=\frac{1}{4}\)
\(\Rightarrow u_n=u_1.q^{n-1}=\frac{3}{4^{n-1}}\)
3/ Không thấy cho n trong khoảng nào, chắc là \(n\ge0\)?
\(u_n=\frac{3n+7-6}{3n+7}=1-\frac{6}{3n+7}< 1\)
\(u_n+\frac{1}{7}=\frac{3n-1}{3n+7}+\frac{1}{7}=\frac{24n}{7\left(3n+7\right)}\ge0\Rightarrow u_n\ge-\frac{1}{7}\)
\(\Rightarrow-\frac{1}{7}\le u_n< 1\Rightarrow u_n\) là dãy bị chặn (bị chặn cả trên lẫn dưới)

a) Ta có \(f\left( x \right),g\left( x \right)\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)
Vậy các hàm số \(f\left( x \right),g\left( x \right)\) liên tục tại \(x = 2\)
b) \(\begin{array}{l}f\left( x \right) + g\left( x \right) = {x^3} + {x^2} + x + 1\\f\left( x \right) - g\left( x \right) = {x^3} - {x^2} + x - 1\\f\left( x \right).g\left( x \right) = \left( {{x^3} + x} \right)\left( {{x^2} + 1} \right) = {x^5} + 2{x^3} + x\\\frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{{x^3} + x}}{{{x^2} + 1}} = \frac{{x\left( {{x^2} + 1} \right)}}{{{x^2} + 1}} = x\end{array}\)
Ta có \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)
Vậy các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại \(x = 2\)

Gọi \(I\left(-1;2\right)\) là tâm đường tròn (C)
\(\overrightarrow{AB}=\left(2;2\right)\)
Gọi I' là ảnh của I qua phép tịnh tiến \(\overrightarrow{AB}\Rightarrow I'\left(1;4\right)\)
Phương trình (C') là ảnh của (C) qua phép tịnh tiến nói trên là:
\(\left(x-1\right)^2+\left(y-4\right)^2=4\)

\(=lim\frac{\left(2+\frac{1}{n}\right)\left(1+\frac{n}{3}\right)\left(n-\frac{11}{n}\right)}{\left(1+\frac{1}{n}\right)\left(1+\frac{2}{n}\right)\left(1-\frac{5}{n}\right)}=\frac{\infty}{1}=+\infty\)

\(v\left(1\right)=2.1=2\\ v\left(2\right)=2.2=4\\ v\left(3\right)=2.3=6\\ v\left(4\right)=2.4=8\\ v\left(5\right)=2.5=10.\)