Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\left(d\right):y=\left(m-2\right)x+m+3\)
Gọi \(A\left(x_o;y_o\right)\) là điểm cố định mà \(\left(d\right)\) đi qua, nên ta có :
\(y_o=\left(m-2\right)x_o+m+3,\forall m\in R\)
\(\Leftrightarrow y_o=mx_o-2x_o+m+3,\forall m\in R\)
\(\Leftrightarrow mx_o+m+2x_o+y_o-3=0,\forall m\in R\)
\(\Leftrightarrow\left(x_o+1\right)m+\left(2x_o+y_o-3\right)=0,\forall m\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_o+1=0\\2x_o+y_o-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_o=-1\\y_o=5\end{matrix}\right.\) \(\Rightarrow A\left(-1;5\right)\)
Vậy Với mọi m, đường thẳng \(\left(d\right)\) luôn đi qua điểm cố định \(A\left(-1;5\right)\)
b) Gọi \(\left\{{}\begin{matrix}\left(d\right)\cap Ox=A\\\left(d\right)\cap Oy=B\end{matrix}\right.\)
Tọa độ điểm \(A\) thỏa mãn
\(\Leftrightarrow\left\{{}\begin{matrix}y=0\\y=\left(m-2\right)x+m+3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+3}{2-m}\\y=0\end{matrix}\right.\)
\(\Rightarrow A\left(\dfrac{m+3}{2-m};0\right)\)
\(\Rightarrow OA=\sqrt[]{\left(\dfrac{m+3}{2-m}\right)^2}=\left|\dfrac{m+3}{2-m}\right|\)
Tọa độ điểm \(B\) thỏa mãn
\(\Leftrightarrow\left\{{}\begin{matrix}y=\left(m-2\right)x+m+3\\x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=m+3\end{matrix}\right.\) \(\Rightarrow B\left(0;m+3\right)\)
\(\Rightarrow OB=\sqrt[]{\left(m+3\right)^2}=\left|m+3\right|\)
\(S_{OAB}=2\Leftrightarrow\dfrac{1}{2}OA.OB=2\)
\(\Leftrightarrow\left|\dfrac{m+3}{2-m}\right|.\left|m+3\right|=4\)
\(\Leftrightarrow\left(m+3\right)^2=4\left|2-m\right|\left(1\right)\)
\(TH1:2-m>0\Leftrightarrow m< 2\)
\(\left(1\right)\Leftrightarrow\left(m+3\right)^2=4\left(2-m\right)\)
\(\Leftrightarrow m^2+6m+9=8-4m\)
\(\Leftrightarrow m^2+10m+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-5+2\sqrt[]{6}\left(tm\right)\\m=-5-2\sqrt[]{6}\left(tm\right)\end{matrix}\right.\)
\(TH2:2-m< 0\Leftrightarrow m>2\)
\(\left(1\right)\Leftrightarrow\left(m+3\right)^2=4\left(m-2\right)\)
\(\Leftrightarrow m^2+6m+9=4m-8\)
\(\Leftrightarrow m^2+2m+17=0\)
\(\Leftrightarrow\) Phương trình vô nghiệm
Vậy \(\left[{}\begin{matrix}m=-5+2\sqrt[]{6}\\m=-5-2\sqrt[]{6}\end{matrix}\right.\) thỏa mãn đề bài

b: Để hai đường song song thì m+1=-2
=>m=-3
c: Gọi A,B lần lượt là giao của (d) với trục Ox và Oy
=>A(-3/m+1;0), B(0;3)
=>OA=3/|m+1|; OB=3
1/2*OA*OB=9
=>9/|m+1|=18
=>|m+1|=1/2
=>m=-1/2 hoặc m=-3/2

c) y = (m – 3)x + 2 (m ≠ 3)
Gọi A, B lần lượt là giao điểm của (d) và trục Ox, Oy và tam giác tạo thành là tam giác AOB vuông tại O
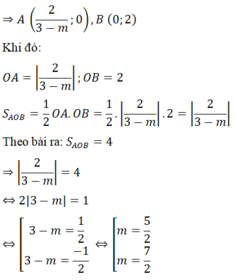

Tọa độ A là;
\(\left\{{}\begin{matrix}y=0\\\left(m+1\right)x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{m+1}\\y=0\end{matrix}\right.\Leftrightarrow OA=\dfrac{3}{\left|m+1\right|}\)
Tọa độ B là:
x=0 và y=(m+1)*0+3=3
=>OB=3
SOAB=9
=>1/2*OA*OB=9
=>1/2*9/|m+1|=9
=>1/2*1/|m+1|=1
=>1/|m+1|=2
=>|m+1|=1/2
=>m+1=1/2 hoặc m+1=-1/2
=>m=-1/2 hoặc m=-3/2
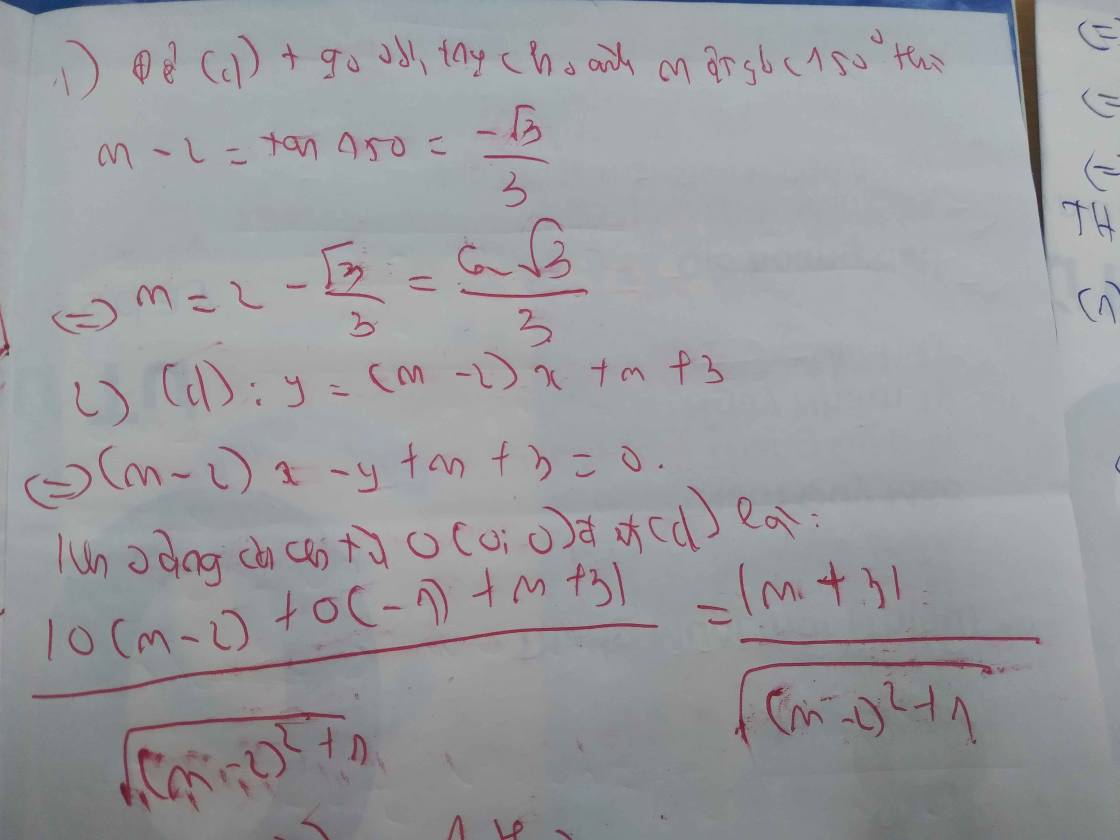
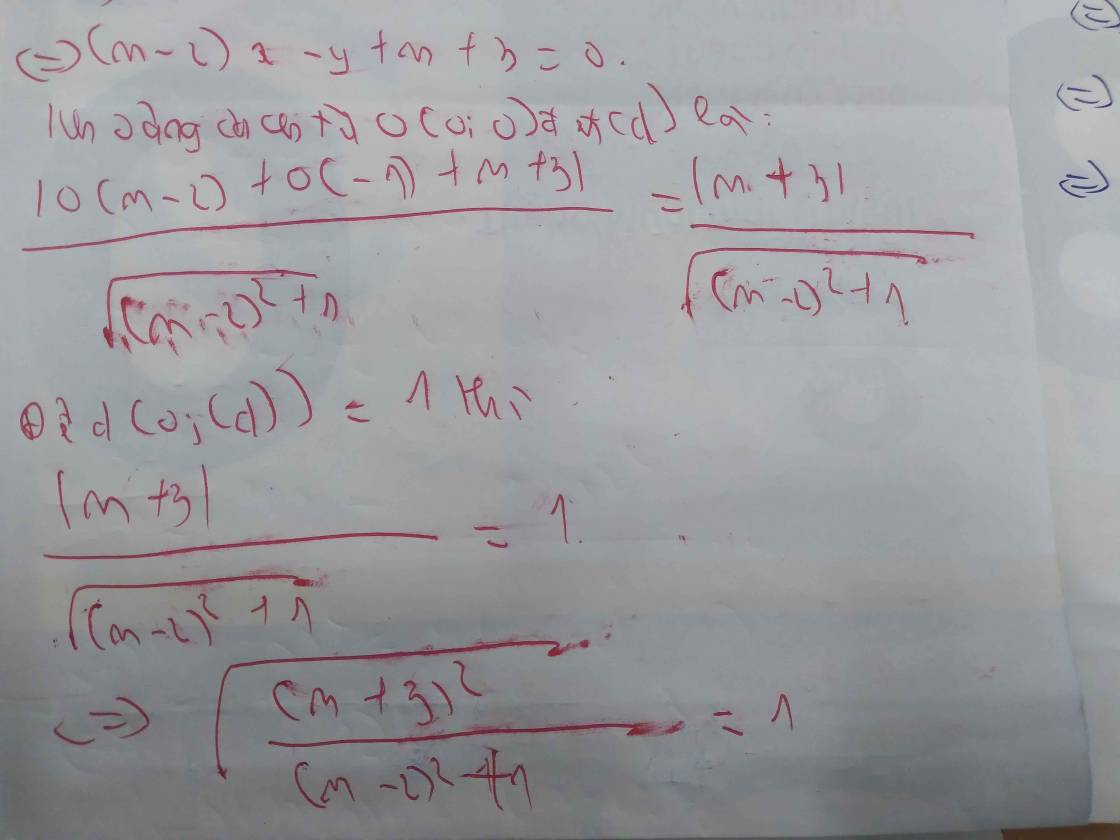





Sửa đề: (d): y=(m-2)x+3
Gọi A,B lần lượt là giao điểm của (d) với trục Ox và trục Oy
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(m-2\right)x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x\left(m-2\right)=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{3}{m-2}\\y=0\end{matrix}\right.\)
=>\(OA=\dfrac{3}{\left|m-2\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m-2\right)x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\left(m-2\right)\cdot0+3=3\end{matrix}\right.\)
=>OB=3
Để \(S_{AOB}=2\) thì \(\dfrac{1}{2}\cdot OA\cdot OB=2\)
=>\(\dfrac{1}{2}\cdot3\cdot\dfrac{3}{\left|m-2\right|}=2\)
=>\(\dfrac{9}{2\left|m-2\right|}=2\)
=>\(4\left|m-2\right|=9\)
=>\(\left|m-2\right|=\dfrac{9}{4}\)
=>\(\left[{}\begin{matrix}m-2=\dfrac{9}{4}\\m-2=-\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{17}{4}\\m=\dfrac{7}{4}\end{matrix}\right.\)