Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Điều kiện của m để hàm số luôn nghịch biến:
<=> m<1
b) Hàm số y=(m-1)x+m+3 song song với đồ thị hàm số y=-2x+1
<=> m-1=-2
<=> m=-1
Vậy m =-1 thi hàm số y=(m-1)x+m+3 song song với đồ thị hàm số y=-2x+1
c) Thay m=-1 vào đồ thị hàm số y=(m-1)x+m+3
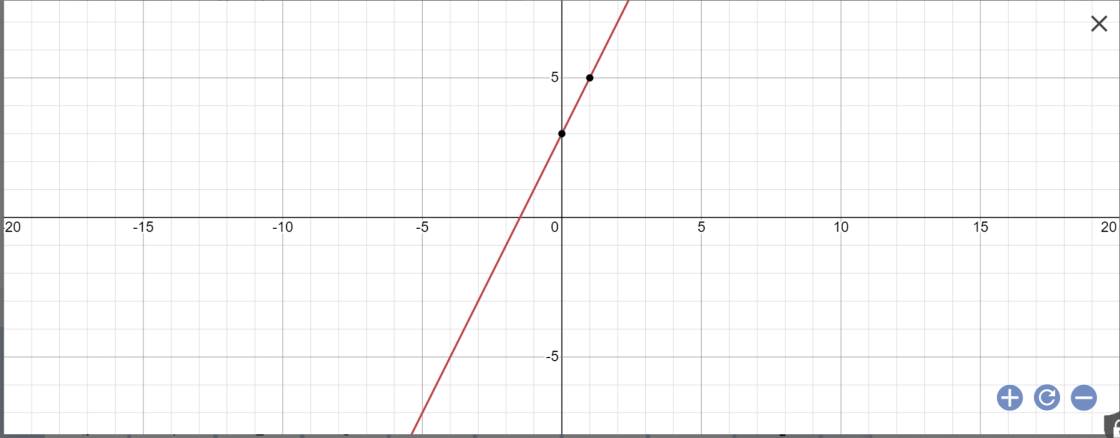
Ta được:y=(-1-2)x-1+3=-2x+2
Đồ thị hàm số y=-2x+2 là đường thẳng đi qua hai điểm (0;2)và (1;0)

a: Để hàm số y=(m-1)x+3 đồng biến trên R thì m-1>0
=>m>1
Để hàm số y=(m-1)x+3 nghịch biến trên R thì m-1<0
=>m<1
b: Thay m=3 vào (d), ta được:
\(y=\left(3-1\right)x+3=2x+3\)
Vẽ đồ thị:
c: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m-1=2\\3\ne-1\left(đúng\right)\end{matrix}\right.\)
=>m-1=2
=>m=3
d: Thay x=-2 và y=0 vào (d1), ta được:
\(-2\left(m-1\right)+3=0\)
=>-2(m-1)=-3
=>\(m-1=\dfrac{3}{2}\)
=>\(m=\dfrac{3}{2}+1=\dfrac{5}{2}\)

a: Để hàm số nghịch biên thì m-2<0
=>m<2
b: Thay x=3 và y=0 vào (d), ta đc:
3(m-2)+m+3=0
=>3m-6+m+3=0
=>4m-3=0
=>m=3/4
c: Tọa độ giao điểm là
2x-1=-x+2 và y=-x+2
=>x=1 và y=1
Thay x=1 và y=1 vào (d), ta được:
m-2+m+3=1
=>2m+1=1
=>m=0

Cho hàm số y = ( m - 2)x + m + 3
a, Tìm điều kiện của m để hàm số luôn nghịch biến
b, Tìm m để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 3
c, Tìm m để đồ thị của hàm số trên và các đồ thị của các hàm số y = -x + 2; y = 2x - 1 đồng quy
Đọc tiếp...
Câu hỏi tương tự Đọc thêm Báo cáo
Toán lớp 9
Để câu trả lời của bạn nhanh chóng được duyệt và hiển thị, hãy gửi câu trả lời đầy đủ và không nên:
- Yêu cầu, gợi ý các bạn khác chọn (k) đúng cho mình
- Chỉ ghi đáp số mà không có lời giải, hoặc nội dung không liên quan đến câu hỏi.
Gửi trả lời Hủy

kem 2k6
Trả lời
2
Đánh dấu
6 phút trước (22:48)
ai lm ny mk ko
mk kem 2k6,kb nha
Tiếng Việt lớp 1
![]()
![]() Missy Girl 4 phút trước (22:49)
Missy Girl 4 phút trước (22:49)
Thống kê hỏi đáp
Báo cáo sai phạm
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
# MissyGirl #
Đọc tiếp...
Đúng 0 Sai 0

Nisaki
Trả lời
1
Đánh dấu
7 phút trước (22:47)
Trong hệ trục tọa độ Oxy cho hàm số y = 3x + m
a, Tính giá trị của m để đồ thị hàm số đi qua : a) A(-1;3) ; B(-2;5)
b, Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ là -3
c, Tìm m để đồ thị hàm số cắt trục tung tại điểm có trung độ là -5
Đọc tiếp...
Toán lớp 9
![]()

Huyền Bùi
Trả lời
1
Đánh dấu
8 phút trước (22:45)
Giai phương trình √8x+1+√46−10x=−x3+5x2+4x+1
Toán lớp 9
![]()
![]() Nguyễn Minh Anh 3 phút trước (22:50)
Nguyễn Minh Anh 3 phút trước (22:50)
Thống kê hỏi đáp
Báo cáo sai phạm
....
- giải
- giải
- giải
=> x =1
- bằng mấy nx thì không biết ...
Đọc tiếp...
Đúng 0 Sai 0

Nisaki
Trả lời
0
Đánh dấu
12 phút trước (22:41)
Cho hàm số y = (m-1)x + m (1)
a, Xác định giá trị của m đường thẳng (1) đi qua gốc tọa độ? Cắt trục tung tại điểm có tung độ bằng 1 - √2
b, Xác định giá trị của m để đường thẳng (1) song song với đường thằng y = -5x + 1
c, Với giá trị nào của m thì góc tạo bởi đườngt hẳng (1) với tia Ox là góc tù? Góc 45 độ
Đọc tiếp...
Toán lớp 9
![]()

Thu Thủy vũ
Trả lời
3
Đánh dấu
2 giờ trước (20:16)
Phân tích đa thức thành nhân tử:
3xy2−2xy+12x
Toán lớp 8
![]()
![]() Đình Sang Bùi 2 giờ trước (20:19)
Đình Sang Bùi 2 giờ trước (20:19)
Thống kê hỏi đáp
Báo cáo sai phạm
Có sai đề không bạn
Đúng 0 Sai 0
![]() Pham Van Hung 2 giờ trước (20:18)
Pham Van Hung 2 giờ trước (20:18)
Thống kê hỏi đáp
Báo cáo sai phạm
3xy2−2xy+12x
=x(3y2−2y+12)
Đúng 0 Sai 0

Nguyen Thu Trang
Trả lời
2
Đánh dấu
28/03/2018 lúc 18:44
Đặt câu để từ kén đc dùng với các nghĩa sau:
A) tổ của con tằm:
B)hành động lựa chọn:
C)có tính chất lựa chọn kĩ:
Đọc tiếp...
Được cập nhật 13 phút trước (22:41)
Tiếng Việt lớp 5
![]()
![]() Lê Diệu Linh 28/03/2018 lúc 18:50
Lê Diệu Linh 28/03/2018 lúc 18:50
Thống kê hỏi đáp
Báo cáo sai phạm
- Con tằm đang nằm trong kén
- Vua Hùng đang kén rể
- Cô ấy rất kén chọn
Đúng 2 Sai 0 Nguyen Thu Trang đã chọn câu trả lời này.

marivan2016
Trả lời
0
Đánh dấu
14 phút trước (22:40)
a) Cho a+b=2. Tìm giá trị nhỏ nhất của A=a2 +b2
b) Cho x+2y=8. Tìm giá trị lớn nhất của B= xy
Toán lớp 9
![]()

marivan2016
Trả lời
0
Đánh dấu
15 phút trước (22:39)
Cho hình vuông OABC cạnh a. Đường tròn tâm O, bán kính a cắt OB tại M. D là điểm đối xứng của O qua C. Đường thẳng Dx vuông góc với CD tại D cắt CM tại E. CA cắt Dx tại F. Đặt α=^MDC
a) chứng minh CM là tia phân giác của góc ACB, Tính độ dài DM, CE theo a và α
b) Tính độ dài CM theo a. Suy ra giá trị của sinα
Đọc tiếp...
Toán lớp 9
![]()

minh tâm lưu
Trả lời
2
Đánh dấu
18 phút trước (22:35)
Tìm từ có tiếng bình điền vào chỗ trống cho thích hợp
- dù sao việc cũng đã thế rồi , mong bác ...................
- giờ đây mọi việc đã ................ trở lại , không bị xáo trộn như mấy tháng trước nữa
các bạn giúp mình nha mình k cho
Đọc tiếp...
Tiếng Việt lớp 5
![]()
![]() Missy Girl 3 phút trước (22:50)
Missy Girl 3 phút trước (22:50)
Thống kê hỏi đáp
Báo cáo sai phạm
- Dù sao việc cũng đã thế rồi , mong bác bình tĩnh .
- Giờ đây mọi việc đã bình yên trở lại , không bị xáo trộn như mấy tháng trước nữa .
...
Ko chắc chắn
Hok tốt
# MissyGirl #
Đọc tiếp...
Đúng 0 Sai 0
![]() ngocanh nguyen 7 phút trước (22:46)
ngocanh nguyen 7 phút trước (22:46)
Thống kê hỏi đáp
Báo cáo sai phạm
- BÌNH TĨNH HOẶC BÌNH TÂM
- BÌNH YÊN
NHỚ KB VÀ K CHO MÌN NHA ! CHÚC HỌC TỐT !
Đúng 0 Sai 0

Phan Hoàng Bảo Ngọc
Trả lời
1
Đánh dấu
30/07/2018 lúc 20:22
phân tích các đa thức sau thành nhân tử tổng hợp x^6-x^4+2x^3+2x
Được cập nhật 20 phút trước (22:33)
Toán lớp 8
![]()
![]() Đường Quỳnh Giang CTV 30/07/2018 lúc 20:25
Đường Quỳnh Giang CTV 30/07/2018 lúc 20:25
Thống kê hỏi đáp
Báo cáo sai phạm
x6−x4+2x3+2x
=x(x5−x3+2x2+2)
p/s: chúc bạn học tốt
Đúng 1 Sai 0

Hoàng Thị Thanh Nhàn
Trả lời
1
Đánh dấu
20 phút trước (22:33)
giải phương trình sau
33√x−2=−6
Toán lớp 9
![]()
![]() Nguyễn Minh Anh 12 phút trước (22:41)
Nguyễn Minh Anh 12 phút trước (22:41)
Thống kê hỏi đáp
Báo cáo sai phạm
33√x−2=−6
⇔√x−2=−29
Vì căn ( x - 2 ) luôn luôn lớn hơn hoặc bằng 0
Nên pt trên vô nghiệm
Đọc tiếp...
Đúng 0 Sai 0

sky mtp
Trả lời
0
Đánh dấu
09/08/2017 lúc 09:40
1.
giải phương trình: √8x+1+√46x−10=x3+5x2+4x+1
Được cập nhật 21 phút trước (22:32)
Toán lớp 9
![]()

Hoàng Thị Thanh Nhàn
Trả lời
0
Đánh dấu
22 phút trước (22:31)
A=(√x+1√x−1 )+2√x+21−x
Tìm điều kiện xác định
Rút gọn A
Đọc tiếp...
Toán lớp 9
![]()

Đặng Anh Thư
Trả lời
1
Đánh dấu
26/09/2017 lúc 14:57
1/ cho tam giác ABC cân đỉnh A. đường cao BE;CF cắt nhau tại H. D là tru...
Cho hàm số y = 2x – 2
a) Vẽ đồ thị của hàm số trên
b) Tìm điểm thuộc thuộc đồ thị hàm số trên có hoành độ bằng 0,5

a) Đề hàm số nghịch biến thì a - 3 < 0 \(\Leftrightarrow a< 3\).
b) Hàm số đi qua điểm M (1; -2 ) nên: \(\left(a-3\right).1-3=-2\)\(\Leftrightarrow a-3=1\)\(\Leftrightarrow a=4\).
c) Đồ thị hàm số là một đường thẳng song song với đường thẳng y = 3x nên \(a-3=3\Leftrightarrow a=6\).

b) thay x=1 , y=-2 vào phương trình f(x) , ta có : \(\left(a-3\right)\times1-3=-2\Leftrightarrow a-3=1\Leftrightarrow a=4\)
c) đồ thị hàm số song song với đường thẳng y=3x , suy ra : \(a-3=3\Leftrightarrow a=6\)

1. hàm số nghịch biến khi
\(a< 0\\ \Leftrightarrow m-2< 0\\ \Leftrightarrow m< 2\)
2. \(y=\left(m-2\right)x+m+3\cap Ox,tại,x=3\)
\(\Rightarrow y=0\)
Có: \(0=\left(m-2\right)3+m+3\\ \Leftrightarrow0=4m-4\\ \Leftrightarrow m=\dfrac{3}{4}\)
3. pt hoành độ giao điểm của
\(y=-x+2,và,y=2x-1\) là
\(-x+2=2x-1\\ \Leftrightarrow3x=3\Leftrightarrow x=1\Rightarrow y=1\)
A(1,1)
3 đt đồng quy \(\Rightarrow A\in y=\left(m-2\right)x+m+3\\ \Rightarrow1=\left(m-2\right)1+m+3\\ \Leftrightarrow2m=0\\ \Leftrightarrow m=0\)
ai trả lời giùm vs ạ cần gấp lắm