Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Đặt t = -sinx + 2 vì ![]() Xét hàm số y = f(t) với
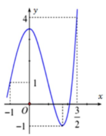
Xét hàm số y = f(t) với ![]() từ đồ thị đã cho, ta có:
từ đồ thị đã cho, ta có:
![]()
![]()

Chọn đáp án D.
Đặt t = - sin x + 2 vì - 1 ≤ sin x ≤ 1
⇒ t ∈ - 1 ; 3
Do đó
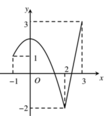
M = m a x [ - 1 ; 3 ] f t = f 3 = 3
m i n [ - 1 ; 3 ] f t = f 2 = - 2 ⇒ M - m = 5

Đáp án D
Phương pháp:
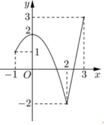
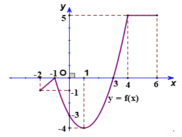
Dựa vào đồ thị hàm số ta xác định được điểm cao nhất và điểm thấp nhất của đồ thị trên đoạn [-1;3]
Tung độ điểm cao nhất là giá trị lớn nhất của hàm số, tung độ điểm thấp nhất là giá trị nhỏ nhất của hàm số trên đoạn [-1;3].
Từ đó ta tìm được: M;m => M-m
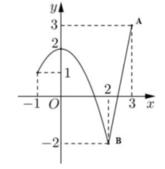
Cách giải:
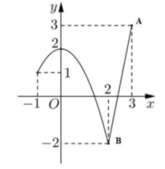
Từ đồ thị hàm số ta thấy trên đoạn [-1;3] thì điểm cao nhất của đồ thị là điểm A(3;3) và điểm thấp nhất của đồ thị là B(2;-2) nên GTLN của hàm số là M=3 và GTNN của hàm số là m = -2
Từ đó M - m = 3 - (-2) = 5

đáp án:
Hàm số đã cho xác định trên D = R.
Với m = -1. Khi đó hàm số trở thành y = -2x + 4 ; y' = -2 < 0 ∀x∈R, không thỏa mãn yêu cầu bài toán.
Với m ≠ -1. Ta có f'(x)= 3(m+1)x2 - 6(m + 1)x + 2m
+ Hàm số đồng biến trên khoảng có độ dài không nhỏ hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn [x1;x2 ] thỏa mãn |x1 - x2 | ≥ 1
+ f'(x)= 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn[x1;x2]
Theo Viét ta có
+ Với |x1 - x2 | ≥ 1 ⇔ (x1 + x2 )2 - 4x1 x2 - 1 ≥ 0
Đối chiếu điều kiện ta có m ≤ -9.
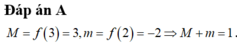
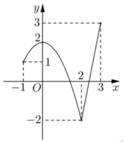
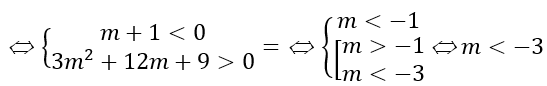
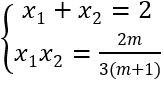
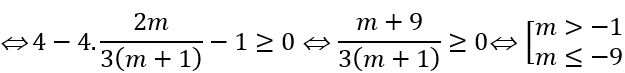
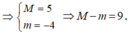
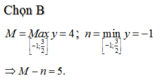
Đáp án C