Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
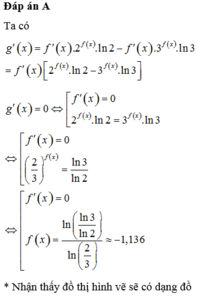
a) Tập xác định : D = R
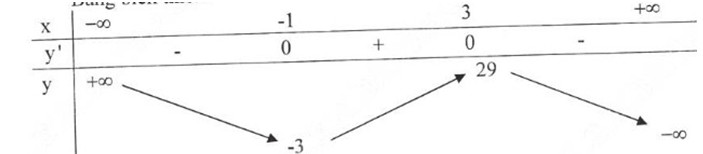
limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3
Bảng biến thiên:
Đồ thị hàm số:
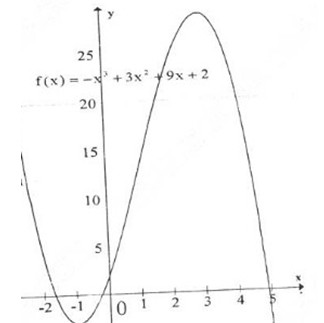
b) y=f(x) = f(x) = -x3+3x2+9x+2.
f’(x) = -3x2+6x+9. Do đó:
f’(x-1)=-3(x-1)2+6(x-1)+9
= -3x2 + 12x = -3x(x-4) > 0 ⇔ 0 < x < 4
c) f’’(x) = -6x+6
f’’(x0) = -6 ⇔ -6x0 + 6 = -6 ⇔ x0 = 2
Do đó: f’(2) = 9, f(2) = 24. Phương trình tiếp tuyến của (C) tại x0 = 2 là:
y=f’(2)(x-2) + f(2) hay y = 9x+6
a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
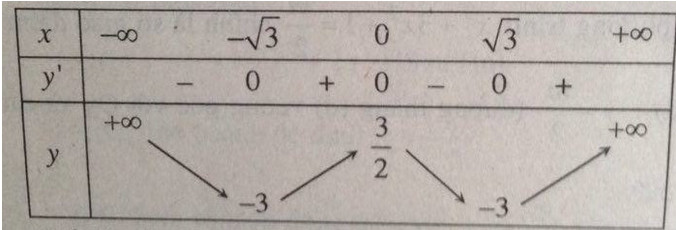
Đồ thị hàm số:
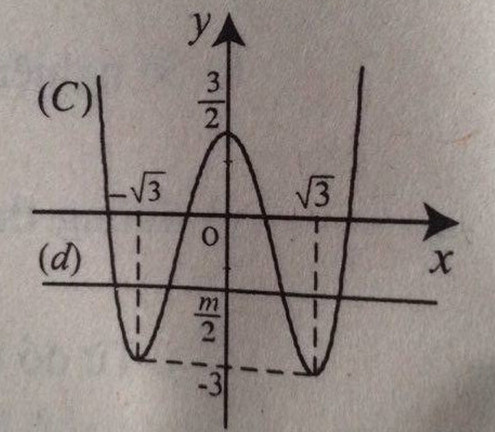
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm
Đáp án B
Ta có
.
.
Hình bên dưới là đồ thị của hàm số 
và 
.
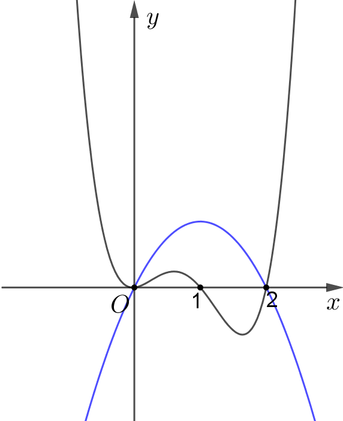
Dựa vào hình vẽ ta thấy đồ thị hàm số 
và 
cắt nhau tại 2 điểm phân biệt, đồng thời 
khi 
hoặc 
, 
khi 
.
Do đó 
đổi dấu qua 
, 
.
Vậy hàm số g(x) có hai điểm cực trị.
.
có 8 nghiệm phân biệt.
