Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
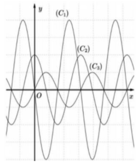
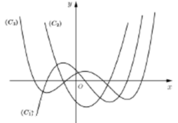
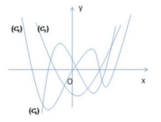
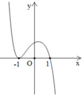
Dựa vào hình vẽ, ta thấy rằng:
Đồ thị C 3 có dạng đồ thị hàm số trùng phương.
Đồ thị C 2 có dạng đồ thị hàm số bậc hai (parabol)
Đồ thị C 1 có dạng đồ thị hàm số bậc ba
Vậy đồ thị của các hàm số
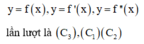

Đáp án C
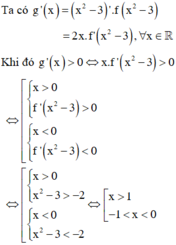
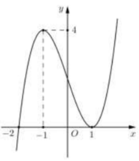
Suy ra hàm số đồng biến trên khoảng (-1;0) và 1 ; + ∞

B
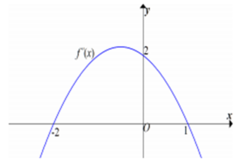
Từ đồ thị của hàm số f"(x) ta có bảng biến
thiên của hàm số f'(x) như sau:
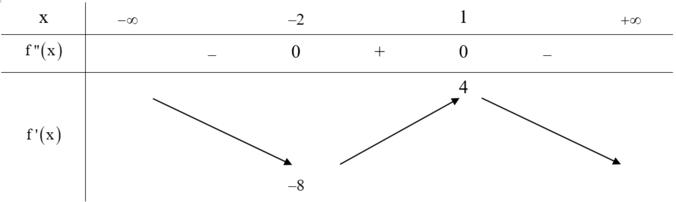

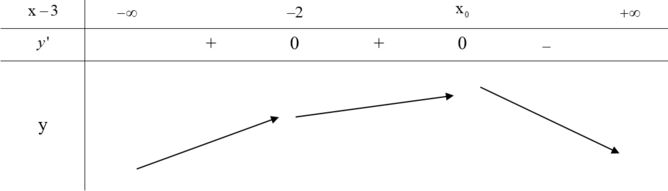
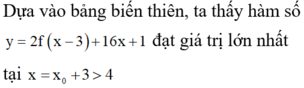

Với hàm số y=f(-2x+1) có
![]()
![]()
![]()
Với hàm số y=g(ax+b) có
y'=a.g'(ax+b)>0 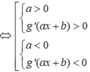
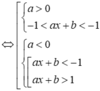
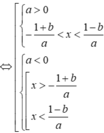
Vì hai hàm số đã cho có cùng khoảng đồng biến nên rơi vào trường hợp
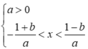 và
và 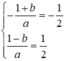
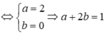
*Chú ý đồ thị đi lên hàm số đồng biến; đồ thị đi xuống hàm số nghịch biến.
Chọn đáp án C.

Đáp án C.
Ta có ![]() ∀
x
∈
R
∀
x
∈
R
Khi đó ![]()
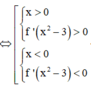
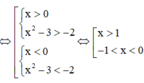
Suy ra hàm số đồng biến trên khoảng (–1;0) và (1;+ ∞)

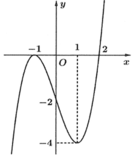
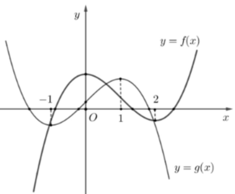
g’(x)=2f(x).f’(x)-4.f’(x)=2f’(x).[f(x)-2]
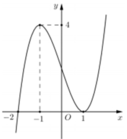
Từ đồ thị trên của y=f’(x) suy ra BBT của y=f(x). Suy ra max f(x)=f(1)=1
Do đó f(x)-2< 0, x ϵ R
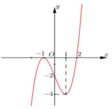
g’(x)=0→f’(x)=0→x= -1 hoặc x=1.
Lập bảng biến thiên suy ra min g(x)= -3
Đáp án A


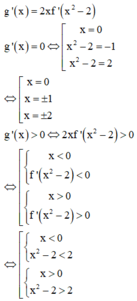
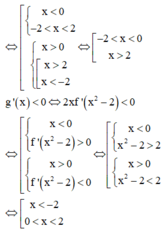

Đáp án là C
Các đồ thị hình vẽ bên chính là đồ thị của các hàm số lượng giác.