Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

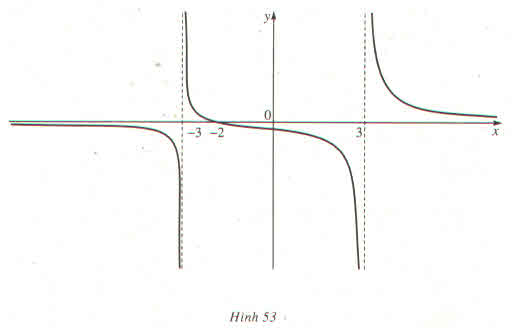
Quan sát đồ thị ta thấy x → -∞ thì f(x) → 0; khi x → 3- thì f(x) → -∞;
khi x → -3+ thì f(x) x → +∞.
b) f(x) =
=
= 0.
f(x) =
=
= -∞ vì
=
> 0 và
= -∞.
f(x) =
=
.
= +∞
vì
=
=
> 0 và
= +∞.

3.
Hàm trùng phương \(f\left(x\right)=ax^4+bx^2+c\) với \(a\ne0\) đồng biến trên \(\left(0;+\infty\right)\) khi và chỉ khi:
\(\left\{{}\begin{matrix}a>0\\b\ge0\end{matrix}\right.\) \(\Leftrightarrow m\ge0\)
Hoặc giải bt: \(y'=4x^3+2mx\ge0\) ;\(\forall x>0\)
\(\Leftrightarrow2x\left(x^2+m\right)\ge0\)
\(\Leftrightarrow x^2+m\ge0\)
\(\Leftrightarrow x^2\ge-m\)
\(\Leftrightarrow-m\le min\left(x^2\right)=0\Rightarrow m\ge0\)
1.
Giả sử tiếp tuyến d có 1 vtpt là \(\left(a;b\right)\) với \(a^2+b^2>0\)
\(\Rightarrow cos30^0=\frac{\sqrt{3}}{2}=\frac{\left|a-2b\right|}{\sqrt{\left(a^2+b^2\right)\left(1^2+\left(-2\right)^2\right)}}=\frac{\left|a-2b\right|}{\sqrt{5\left(a^2+b^2\right)}}\)
\(\Leftrightarrow4\left(a-2b\right)^2=15\left(a^2+b^2\right)\)
\(\Leftrightarrow11a^2+16ab-b^2=0\)
Nghiệm xấu quá nhìn muốn nản, bạn tự làm tiếp :)
2.
\(y'=cosx-2sinx+2m-5\)
Hàm số đồng biến trên TXĐ khi và chỉ khi \(y'\ge0\) ; \(\forall x\)
\(\Leftrightarrow cosx-2sinx+2m-5\ge0\) ;\(\forall x\)
\(\Leftrightarrow2m-5\ge2sinx-cosx\)
\(\Leftrightarrow2m-5\ge f\left(x\right)_{max}\) với \(f\left(x\right)=2sinx-cosx\)
Ta có: \(f\left(x\right)=2sinx-cosx=\sqrt{5}\left(\frac{2}{\sqrt{5}}sinx-\frac{1}{\sqrt{5}}cosx\right)=\sqrt{5}sin\left(x-a\right)\)
Với \(a\in\left(0;\pi\right)\) sao cho \(cosa=\frac{2}{\sqrt{5}}\)
\(\Rightarrow f\left(x\right)\le\sqrt{5}\Rightarrow2m-5\ge\sqrt{5}\Rightarrow m\ge\frac{5+\sqrt{5}}{2}\)

\(y'=x^2-2\left(m-1\right)x+3\left(m-1\right)\)
Hàm đồng biến trên khoảng đã cho khi với mọi \(x>1\) ta luôn có:
\(g\left(x\right)=x^2-2\left(m-1\right)x+3\left(m-1\right)\ge0\)
\(\Rightarrow\min\limits_{x>1}g\left(x\right)\ge0\)
Do \(a=1>0;-\dfrac{b}{2a}=m-1\)
TH1: \(m-1\ge1\Rightarrow m\ge2\)
\(\Rightarrow g\left(x\right)_{min}=f\left(m-1\right)=\left(m-1\right)^2-2\left(m-1\right)^2+3\left(m-1\right)\ge0\)
\(\Rightarrow\left(m-1\right)\left(4-m\right)\ge0\Rightarrow1\le m\le4\Rightarrow2\le m\le4\)
TH2: \(m-1< 1\Rightarrow m< 2\Rightarrow g\left(x\right)_{min}=g\left(1\right)=m\ge0\)
Vậy \(0\le m\le4\)