Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2
a)
d đi qua A (1;2), B(2;5)
=> Ta có hệ phương trình: \(\left\{{}\begin{matrix}\left(m-1\right).1+n=2\\\left(m-1\right).2+n=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m+n=3\\2m+n=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=4\\n=-1\end{matrix}\right.\)
b)
d có hệ số góc a = 3 => d: y = 3x + n
=> m -1 = 3 <=> m = 4
d cắt Ox tại x = -2, y = 0 \(\Leftrightarrow0=3.\left(-2\right)+n\) => n = 6
c)
d trùng d' \(\Rightarrow\left\{{}\begin{matrix}m-1=5\\n=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=6\\n=-3\end{matrix}\right.\)

a> gọi y=(m-2)x+n là (d)
để (d) là hsbn thì m khác 2, với mọi n thuộc R
b> hàm số đồng biến khi m>2
nghịch biến khi m<2
c> điều kiện để (d) // (d'): y=2x-1 <=> m-2=2 <=>m=4
và n khác -1
vậy để (d) // (d') <=> m=4, m khác 2, n khác -1
d> điều kiện để (d) cắt (d''): y=-3x+2 <=> m-2=-3 <=> m khác -1
vậy để (d) cắt (d'') <=> m khác 2, m khác -1
e> để (d) trùng (d'''): y=3x-2 <=> m-2=3 <=> m=5
và n = -2
vậy để d//d''' <=> m khác 2, m=5, n=-2
f> vì d đi qua A(1;2) => 2=m-2+n <=> m+n=4 (1). vì d đi qua B(3;4) => 4=3m-6+n <=> 3m+n = 10 (2)
lấy (2) trừ (1) <=> 2m=6 <=> m= 3 => n=1

a. Để hs (1) đồng biến trên R :
\(\Leftrightarrow-m-18>0\)
\(\Leftrightarrow-m>18\)
\(\Leftrightarrow m< -18\)
Vậy \(m< -18\) thì hs (1) đồng biến trên R
b. Do ĐTHS (1) // đ.t \(y=-19x-5\) nên :
\(\left\{{}\begin{matrix}-m-18=-19\\3m+1\ne-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m\ne-2\end{matrix}\right.\)
c. Vì ĐTHS (1) đi qua điểm \(A\left(-1;2\right)\) nên ta có : x = -1 và y = 2
Thay x = -1 và y = 2 vào (1) ta được :
\(2=\left(-m-18\right).\left(-1\right)+3m+1\)
\(\Leftrightarrow2=m+18+3m+1\)
\(\Leftrightarrow-17=4m\)
\(\Leftrightarrow m=\dfrac{-17}{4}\)
a. hàm số (1) đồng biến trên R khi -m-18 > 0 <=> m < -18 . Vậy m < -18 thì hàm số (1) đồng biến. b. đồ thị hàm số (1) song song với đường thẳng y= -19x-5 <=> -m-18=-19 và 3m+1 khác -5 <=> m= 1 và m khác 4/3 . Vậy m=1 và m khác 4/3 thì đồ thị hàm số ( 1 ) song song với đường thẳng y= -19x-5 . c. đồ thị hàm số y=(-m-18)x+3m+1 đi qua A(-1;2) => x=-1 ; y=2 => 2=(-m-18)*(-1)+3m+1 <=> 2= m+18+3m+1 <=> 4m=17 <=> m=17/4 . Vậy m=17/4 thì đồ thị hàm số y=(-m-18)x+3m+1 đi qua A(-1;2)

a: Để hàm số đồng biến thì m-3>0
=>m>3
b: Vì (d) đi qua O(0;0) và B(-1;2) nên ta có hệ:
0(m-3)+n=0 và -(m-3)+n=2
=>n=0 và m-3=-2
=>m=1 và n=0
c: Vì (d)//y=x-2 nên m-3=1
=>m=4
=>(d): y=x+n
Thay x=0 và y=5 vào (d), ta được:
n+0=5
=>n=5
=>(d): y=x+5
d: Vì (d) đi qua A(2;1) và B(3;0) nên ta có hệ:
2(m-3)+n=1 và 3(m-3)+n=0
=>2m-6+n=1 và 3m-9+n=0
=>2m+n=7 và 3m+n=9
=>m=2 và n=3

1) Để (d) cắt trục tung tại điểm có tung độ là -1 nên Thay x=0 và y=-1 vào hàm số y=(2m-1)x-3m+5, ta được:
\(\left(2m-1\right)\cdot0-3m+5=-1\)
\(\Leftrightarrow-3m+5=-1\)
\(\Leftrightarrow-3m=-1-5=-6\)
hay m=2(nhận)
Vậy: Khi m=2 thì (d) cắt trục tung tung tại điểm có tung độ bằng -1

a) Vì đồ thị hàm số y=ax+b vuông góc với đồ thị hàm số \(y=\dfrac{1}{3}x-1\) nên \(a\cdot\dfrac{1}{3}=-1\)
\(\Leftrightarrow a=-1:\dfrac{1}{3}=-1\cdot\dfrac{3}{1}=-3\)
Vậy: Hàm số có dạng y=-3x+b
Vì đồ thị hàm số y=-3x+b đi qua điểm A(1;2) nên
Thay x=1 và y=2 vào hàm số y=-3x+b, ta được:
\(-3\cdot1+b=2\)
\(\Leftrightarrow b-3=2\)
hay b=5
Vậy: Hàm số có dạng y=-3x+5

a, với d = -1
Ta có hàm số y = - \(x\) + 4 + 3 ⇒ y = -\(x\) + 7
+ Giao của đồ thị với trục o\(x\) là điểm có hoành độ thỏa mãn:
- \(x\) + 7 = 0 ⇒ \(x\) = 7
Giao đồ thì với trục o\(x\) là A(7; 0)
+ Giao của đồ thị với trục oy là điểm có tung độ thỏa mãn:
y = 0 + 7 ⇒ y = 7
Giao đồ thị với trục oy là điểm B(7; 0)
Ta có đồ thị
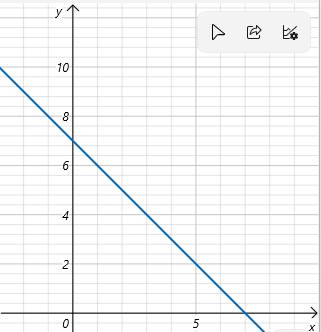
b, Đồ thị hàm số y = - m\(x\) + 4 - 3m (d)
(d) đi qua gốc tọa độ khi và chỉ tọa độ O(0; 0) thỏa mãn phương trình đường thẳng d
Thay tọa độ điểm O vào đường thẳng d ta có:
-m.0 + 4 - 3m = 0
4 - 3m = 0
m = \(\dfrac{4}{3}\)
c, để d cắt trục tung tại điểm - 4 khi và chỉ m thỏa mãn phương trình:
-m.0 + 4 - 3m = - 4
4 - 3m = - 4
3m = 8
m = \(\dfrac{8}{3}\)
d, d cắt trục tung tại điểm - 2 khi và chỉ khi m thỏa mãn phương trình
-m.0 + 4 - 3m = -2
4 - 3m = -2
3m = 6
m = 2
e, d song song với đường thẳng y = 2\(x\) + 3 khi và chỉ khi
- m = 2 và 4 - 3m ≠ 3 ⇒ m ≠ \(\dfrac{1}{3}\)
⇒m = -2
f, d đi qua A (1;2) khi và chỉ m thỏa mãn phương trình:
-m.(1) + 4 - 3m = 2
-m - 3m = 2 - 4
- 4m = -2
m = \(\dfrac{1}{2}\)

b: Vì đồ thị hàm số đi qua hai điểm P(2;1) và Q(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=1\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-3\\b-a=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=4+a=3\end{matrix}\right.\)
a: Vì đồ thị hàm số y=ax+b vuông góc với y=3x+1 nên 3a=-1
hay \(a=-\dfrac{1}{3}\)
Vậy: \(y=-\dfrac{1}{3}x+b\)
Thay x=1 và y=2 vào hàm số, ta được:
\(b-\dfrac{1}{3}=2\)
hay \(b=\dfrac{7}{3}\)
Thay x=2 và y=-9 vào (d), ta được:
2(3m-2)+n-1=-9
=>6m-4+n-1=-9
=>6m+n=-9+5=-4(1)
Thay x=1 và y=2 vào (d), ta được:
1(3m-2)+n-1=2
=>3m-2+n-1=2
=>3m+n=5(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}6m+n=-4\\3m+n=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3m=-9\\3m+n=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}n=5-\left(-9\right)=14\\m=-3\end{matrix}\right.\)