Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=x^2-\left(3m+2\right)x+2m^2+3m+1\)
\(\Delta=\left(3m+2\right)^2-4\left(2m^2+3m+1\right)=m^2\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\frac{3m+2+m}{2}=2m+1\\x_2=\frac{3m+2-m}{2}=m+1\end{matrix}\right.\)
Để hàm số có cực đại, cực tiểu \(\Rightarrow x_1\ne x_2\Rightarrow m\ne0\)
- Nếu \(m>0\Rightarrow2m+1>m+1\Rightarrow\left\{{}\begin{matrix}x_{CĐ}=m+1\\x_{CT}=2m+1\end{matrix}\right.\)
\(\Rightarrow3\left(m+1\right)^2=4\left(2m+1\right)\) \(\Rightarrow3m^2-2m-1=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-\frac{1}{3}< 0\left(l\right)\end{matrix}\right.\)
- Nếu \(m< 0\Rightarrow m+1>2m+1\Rightarrow\left\{{}\begin{matrix}x_{CĐ}=2m+1\\x_{CT}=m+1\end{matrix}\right.\)
\(\Rightarrow3\left(2m+1\right)^2=4\left(m+1\right)\Rightarrow12m^2+8m-1=0\)
\(\Rightarrow\left[{}\begin{matrix}m=\frac{-2+\sqrt{7}}{6}>0\left(l\right)\\m=\frac{-2-\sqrt{7}}{6}\end{matrix}\right.\) \(\Rightarrow\sum m=\frac{4-\sqrt{7}}{6}\)

Câu 2:
$y'=-3x^2+6x+(m-2)=0$
Để hàm số có 2 điểm cực trị $x_1,x_2$ đồng nghĩa với PT $-3x^2+6x+(m-2)=0$ có 2 nghiệm phân biệt $x_1,x_2$
$\Leftrightarrow \Delta'=9+3(m-2)>0\Leftrightarrow m>-1(1)$
Hai điểm cực trị cùng dương khi:
\(\left\{\begin{matrix} x_1+x_2=2>0\\ x_1x_2=\frac{m-2}{-3}>0\end{matrix}\right.\Leftrightarrow m< 2(2)\)
Từ $(1);(2)\Rightarrow -1< m< 2$
Đáp án C.
Câu 2:
Để đths có 2 điểm cực trị thì trước tiên:
$y'=x^2-2mx+m^2-4=0$ có 2 nghiệm phân biệt $x_1,x_2$
Điều này xảy ra khi $\Delta'=m^2-(m^2-4)>0\Leftrightarrow m\in\mathbb{R}$
Để 2 điểm cực trị của đồ thị $y$ nằm về hai phía của trục tung thì: $x_1x_2< 0$
$\Leftrightarrow m^2-4< 0$
$\Leftrightarrow -2< m< 2$
Đáp án A.

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

Lời giải + diễn giải
để hàm có cực trị f'(x) phải có nghiệm và đổi dấu qua nghiệm
a) \(y'=3x^2-6x+m\)
xét f(x)= 3x^2 -6x+m
để f(x) là hàm bậc 2 => có nghiệm và đổi dấu qua nghiệm đk cần và đủ \(\Delta>0\)
\(\Leftrightarrow\Delta'=9-3m>0\Rightarrow m< 3\)
Kết luận với m< 3 hàm A(x) luôn có cực trị
b)
\(y'=3x^2+4mx+m\)
\(\Delta'=4m^2-3m>0\Leftrightarrow\left[{}\begin{matrix}m< 0\\m>\dfrac{3}{4}\end{matrix}\right.\)
c)
\(y=\dfrac{x^2-2mx+5}{x-m}\Rightarrow\left\{{}\begin{matrix}x\ne m\\y=\left(x-m\right)+\dfrac{5-m^2}{x-m}\end{matrix}\right.\)
\(y'=1+\dfrac{m^2-5}{\left(x-m\right)^2}\)
\(y'=0\Leftrightarrow\left(x-m\right)^2+m^2-5=0\Rightarrow5-m^2>0\Rightarrow-\sqrt{5}< m< \sqrt{5}\)

Lời giải:
"3 cực trị" bạn nói hẳn là hoành độ.
Ta có \(y'=x^3+mx^2-x-m=0\)
\(\Leftrightarrow (x+m)(x-1)(x+1)=0\)
Để hàm có ba cực trị thì trước tiên \(m\neq \pm 1\)
Khi đó, hoành độ ba điểm cực trị là \(-1,1,-m\)
TH1 Nếu một cấp số nhân gồm 3 số trên có \(1,-1\) đứng cạnh nhau thì công bội có thể là \(\pm 1\Rightarrow m=\pm 1\) (vô lý)
TH2: \(-m\) nằm giữa.
Giả sử ta có CSN là \(-1,-m,1\) thì \(\left\{\begin{matrix} -m=-1q\\ 1=-mq\end{matrix}\right.\Rightarrow \left\{\begin{matrix} m=q\\ -1=mq\end{matrix}\right.\Rightarrow -1=m^2\) (vô lý)
Tương tự SCN là \(1,-m,-1\) cũng vô lý.
Vậy không có $m$ thỏa mãn

\(y'=3x^2+2x+m+1\)
Để hàm số có 2 cực trị \(\Leftrightarrow\Delta'=1-3\left(m+1\right)>0\Leftrightarrow m< -\frac{2}{3}\)
Khi đó theo Viet: \(\left\{{}\begin{matrix}x_{CĐ}+x_{CT}=-\frac{2}{3}\\x_{CĐ}.x_{CT}=\frac{m+1}{3}\end{matrix}\right.\)
a/ Để biểu thức bài toán xác định \(\Rightarrow m\ne-1\)
\(\frac{x_{CĐ}+x_{CT}}{x_{CĐ}.x_{CT}}=3\Leftrightarrow\frac{-\frac{2}{3}}{\frac{m+1}{3}}=3\Leftrightarrow m+1=-\frac{2}{3}\Rightarrow m=-\frac{5}{3}\)
b/ Để hai cực trị cùng âm \(\Leftrightarrow\left\{{}\begin{matrix}x_{CĐ}+x_{CT}=-\frac{2}{3}< 0\\x_{CĐ}.x_{CT}=m+1>0\end{matrix}\right.\)
\(\Leftrightarrow-1< m< -\frac{2}{3}\)
c/ Do \(x_{CĐ}+x_{CT}=-\frac{2}{3}< 0\) nên ko tồn tại m để hàm số có 2 cực trị cùng dương




+ Ta có đạo hàm y’ = 3x2- 12x+ 3( m+ 2)
Phương trình y’ = 0 khi 3x2- 12x+ 3( m+ 2) = 0
+ Hàm số có 2 điểm cực trị x1; x2 ⇔ Δ’ > 0 ⇔ m < 2
+ Chia y cho y’ ta được :y= 1/3.y’( x-2) + (m-2) (2x+ 1)
Tọa độ 2 điểm cực trị tương ứng : A( x1 ; ( m-2) ( 2x1+ 1) ) và B( x2 ; ( m-2) ( 2x2+ 1) )
+ ta có ; y1.y2= ( m-2) 2( 4x1x2+ 2( x1+ x2) + 1)
Với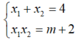 nên: y1y2= ( m-2) 2( 4m+ 17)
nên: y1y2= ( m-2) 2( 4m+ 17)
Hai cực trị cùng dấu khi và chỉ khi y1.y2> 0 hay ( m-2) 2( 4m+ 17) > 0
⇔ m > - 17 4 m ≠ 2
Kết hợp điều kiện ta được : -17/4< m< 2; mà m nguyên nên m= -4; -3; ...0; 1
Có tất cả 6 giá trị nguyên của m thỏa mãn đầu bài.
Chọn C.