Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta có \(y'=3x^2-6mx+3(m+6)=0\) có hai nghiệm $x_1,x_2$ chính là hoành độ hai cực trị của đồ thị hàm số. Theo hệ thức Viet:
\(\left\{\begin{matrix} x_1+x_2=2m\\ x_1x_2=m+6\end{matrix}\right.(1)\)
Gọi đường thẳng qua hai điểm cực trị có PT \((d):y=ax+b\)
Ta có: \(\left\{\begin{matrix} y_1=ax_1+b=x_1^3-3mx_1^2+3(m+6)x_1+1\\ y_2=ax_2+b=x_2^3-3mx_2^2+3(m+6)x_2+1\end{matrix}\right.\)
Dựa vào $(1)$ và biến đổi đơn giản:
\(\Rightarrow a(x_1-x_2)=(x_1-x_2)[x_1^2+x_1x_2+x_2^2-3m(x_1+x_2)+3(m+6)]\)
\(\Rightarrow a=x_1^2+x_1x_2+x_2^2-3m(x_1+x_2)+3(m+6)=-2m^2+2m+12\)
\(\Rightarrow 2b=y_1+y_2-a(x_1+x_2)=2m^2+12m+2\Rightarrow b=m^2+6m+1\)
Do đó PTĐT thu được: \((d):y=(-2m^2+2m+12)x+m^2+6m+1\)

Baif 1:
$y'=3x^2-3=0\Leftrightarrow x=\pm 1$
$x=1\Rightarrow y=-3$
$x=-1\Rightarrow y=1$
Vậy hai điểm cực trị của ĐTHS $y=x^3-3x-1$ là $A(1,-3); B(-1,1)$
$\overrightarrow{AB}=(-2, 4)\Rightarrow \overrightarrow{n_{AB}}=(4,2)$
PTĐT đi qua 2 điểm cực trị $A,B$ là:
$4(x-1)+2(y+3)=0$
$\Leftrightarrow 2x+y+1=0$
Bài 2:
$y'=3x^2-3=0\Leftrightarrow x=\pm 1$
$y(1)=-1$
$y(-1)=3$
Vậy ĐTHS có 2 điểm cực trị $A(1,-1)$ và $B(-1,3)$
$\overrightarrow{AB}=(-2,4)\Rightarrow (4,2)
PTĐT $AB$: $4(x-1)+2(y+1)=0$
$\Leftrightarrow 2x+y-1=0$
d(O,AB)=\frac{|2.0+0-1|}{\sqrt{2^2+1^2}}=\frac{1}{\sqrt{5}}$
$S_{OAB}=\frac{d(O,AB).AB}{2}=\frac{1}{2\sqrt{5}}.\sqrt{(-2)^2+4^2}=1$ (đơn vị diện tích)


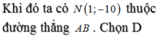
\(y=x^3-6x^2-1\)
\(y'=3x^2-12x\)
Ta có: \(x^3-6x^2-1=\left(3x^2-12x\right)\left(\frac{1}{3}x-\frac{2}{3}\right)-8x-1\)
Do đó phương trình đường thẳng đi qua hai điểm \(A\), \(B\)là \(y=-8x-1\).
Ta lần lượt thử tọa độ các điểm của \(4\)phương án.
Chọn A.