Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Phương pháp:
Giải phương trình hoành độ giao điểm, tìm giao điểm của hai đồ thị.
Dựa vào công thức trọng tâm, xác định m.
Cách giải:
Phương trình hoành độ giao điểm của d và (C) là
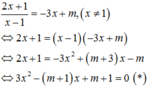
Để d cắt (C) tại hai điểm phân biệt A, B thì (*) có 2 nghiệm phân biệt khác 1
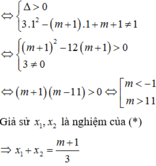


Đáp án C
Phương trình hoành độ của ( C ) và ( d ) là
2 x + 1 x − 1 = m − 3 x ⇔ x ≠ 1 3 x 2 − m + 1 x + m + 1 *
Để ( C ) cắt ( d ) tại 2 điểm phân biệt ⇔ * có 2 nghiệm phân
biệt khác 1 ⇔ m > 11 m < − 1 .
Khi đó, gọi A x 1 ; y 1 , B x 2 ; y 2 là tọa độ giao điểm
⇒ G x 1 + x 2 3 ; y 1 + y 2 3 Mà
y 1 = − 3 x 1 + m y 2 = − 3 x 2 + m ⇒ y 1 + y 2 3 = 2 m − 3 x 1 + x 2 3 = m − 1 3 ⇒ G m + 1 9 ; m − 1 3 .
Theo bài ra, ta có
G ∈ C s u y r a m − 1 3 . m + 1 9 − 1 = 2. m + 1 9 + 1 ⇒ m = 15 ± 5 13 2 .
Kết hợp với điều kiện
m > 11 m < − 1 ⇒ m = 15 + 5 13 2 .

Đáp án D
Phương pháp:
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x o .
+) Tìm giao điểm của tiếp tuyến với các trục tọa độ.
+) Tính OA, OB, giải phương trình tìm x o → Phương trình tiếp tuyến và kết luận.

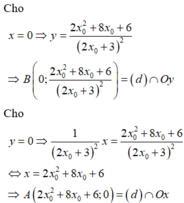
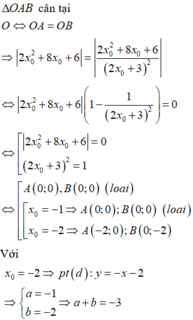


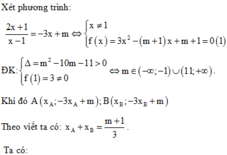
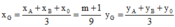
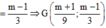
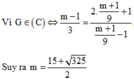

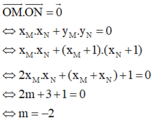




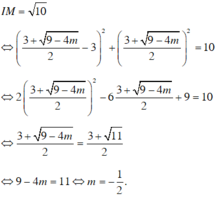



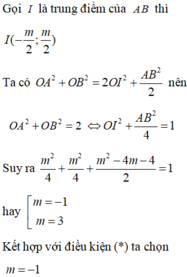
Đáp án D
Phương trình hoành độ giao điểm của C và d là
x x − 1 = m − x ⇔ x ≠ 1 x 2 − m x + m = 0 * .
Để C cắt d tại hai điểm phân biệt ⇔ * có hai nghiệm phân biệt khác 1 ⇔ m > 4 m < 0 .
Khi đó, gọi điểm A x 1 ; m − x 1 và B x 2 ; m − x 2 là giao điểm của đồ thị C và d .
⇒ O A = 2 x 1 2 − 2 m . x 1 + m 2 = 2 x 1 2 − m x 1 + m + m 2 − 2 m = m 2 − 2 m O B = 2 x 2 2 − 2 m . x 2 + m 2 = 2 x 2 2 − m x 2 + m + m 2 − 2 m = m 2 − 2 m
Khoảng cách từ O đến AB bằng
h = d O ; d = m 2 ⇒ S Δ A B C = 1 2 . h . A B = m 2 2 . A B
Ta có
S Δ A B C = a b c 4 R ⇔ R = a b c 4. S Δ A B C = O A . O B . A B 2. h . A B = O A . O B 2. h ⇔ 4 2 . m 2 = O A . O B ⇔ O A 2 . O B 2 = 16 m 2
Khi đó m 2 − 2 m 2 = 16 m 2 ⇔ m 2 − 2 m = 4 m m 2 − 2 m = − 4 m ⇔ m = 0 m = − 2 m = 6 .
Kết hợp với điều kiện m > 4 m < 0 , ta được m = − 2 m = 6 là giá trị cần tìm