Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án: D.
Vì x 2 + x + 4 > 0 với mọi x nên phương trình (x − 3)( x 2 + x + 4) = 0 chỉ có một nghiệm là x = 3. Do đó, đồ thị của hàm số đã cho chỉ có một giao điểm với trục hoành.
Đáp án: D.
Vì x 2 + x + 4 > 0 với mọi x nên phương trình (x − 3)( x 2 + x + 4) = 0 chỉ có một nghiệm là x = 3. Do đó, đồ thị của hàm số đã cho chỉ có một giao điểm với trục hoành.
a) Hàm có cực đại, cực tiểu khi mà $y'=-3x^2+2(m-1)x=x[2(m-1)-3x]$ có ít nhất hai nghiệm phân biệt $\Leftrightarrow 2(m-1)-3x=0$ có một nghiệm khác $0$ hay $m\neq 1$
b) Đồ thị hàm số $(\star)$ cắt trục hoành tại ba điểm phân biệt khi mà phương trình $y=-x^3+(m-1)x^2-m+2=0$ có $3$ nghiệm phân biệt
$\Leftrightarrow (1-x)[x^2+x(2-m)+(2-m)]=0$ có ba nghiệm phân biệt
$\Leftrightarrow x^2+x(2-m)+(2-m)=0$ có hai nghiệm phân biệt khác $1$
Do đó ta cần có $\left\{\begin{matrix}1+2-m+2-m=5-2m\neq 0\\ \Delta =(2-m)^2-4(2-m)>0\end{matrix}\right.$
Vậy để thỏa mãn đề bài thì $m\neq \frac{5}{2}$ và $m>2$ hoặc $m<-2$
c) Gọi điểm cố định mà đồ thị hàm số đi qua là $(x_0,y_0)$
$y_0=-x_0^3+(m-1)x_0^2-m+2$ $\forall m\in\mathbb{R}$
$\Leftrightarrow m(x_0^2-1)-(x_0^3+x_0^2+y_0-2)=0$ $\forall m\in\mathbb{R}$
$\Rightarrow\left{\begin{matrix}x_0^2=1\\ x_0^3+x_0^2+y_02=0\end{matrix}\right.\begin{bmatrix}(x_0,y_0)=(1;0)\\ (x_0,y_0)=(-1;2)\end{bmatrix}$
Viết lại đoạn cuối:
$\Rightarrow\left{\begin{matrix}x_0^2=1\\x_0^3+x_0^2+y_0-2=0\end{matrix}\right.$ $\Rightarrow \begin{bmatrix}(x_0,y_0)=(1;0)\\ (x_0,y_0)=(-1;2)\end{bmatrix}$
a) Học sinh tự giải
b)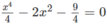 
⇔ x 4 − 8 x 2 − 9 = 0
⇔ ( x 2 + 1)( x 2 − 9) = 0
⇔ 
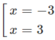
(C) cắt trục Ox tại x = -3 và x = 3
Ta có: y′ = x 3 − 4x
Phương trình tiếp tuyến của (C) tại điểm có hoành độ x = 3 và x = -3 lần lượt là:
y = y′(3)(x – 3) và y = y′(−3)(x + 3)
Hay y = 15(x – 3) và y = −15(x + 3)
c)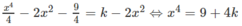 
Từ đó, ta có:
k = −9/4: (C) và (P) có một điểm chung là (0; −9/4)
k > −9/4: (C) và (P) có hai giao điểm.
k < −9/4: (C) và (P) không cắt nhau.
\(k>-\dfrac{9}{4}:\) (C) và (P) có hai giao điểm
\(k< -\dfrac{9}{4}:\) (C) và (P) không cắt nhau
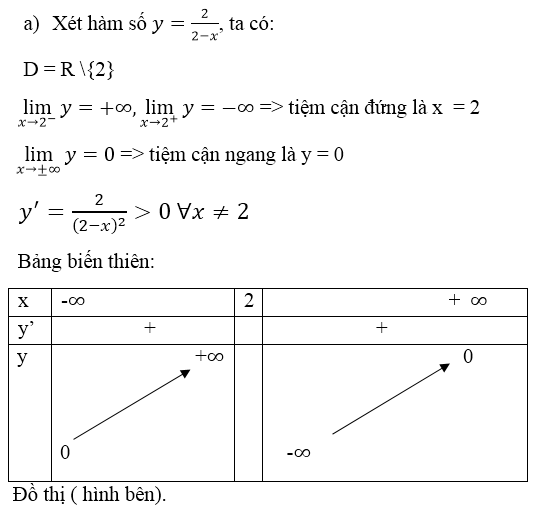
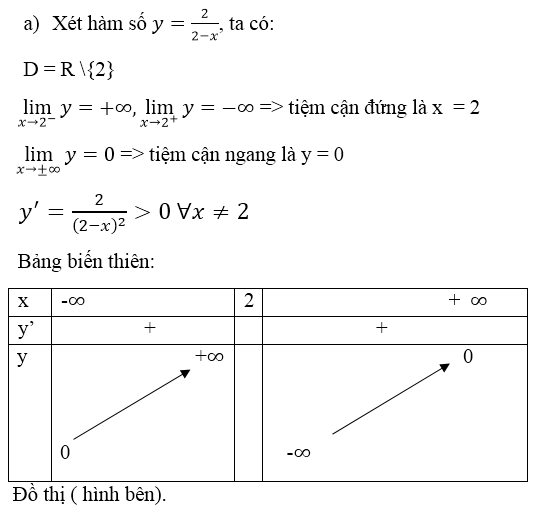
a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)
Ta có
Đồ thị hàm số 
cắt trục hoành tại bốn điểm phân biệt bên phương trình 
, với 
là các nghiệm.
Suy ra
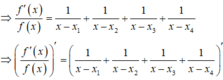
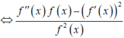
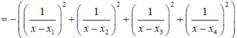
Nếu 
với 
thì 
, 
.
Nếu 
thì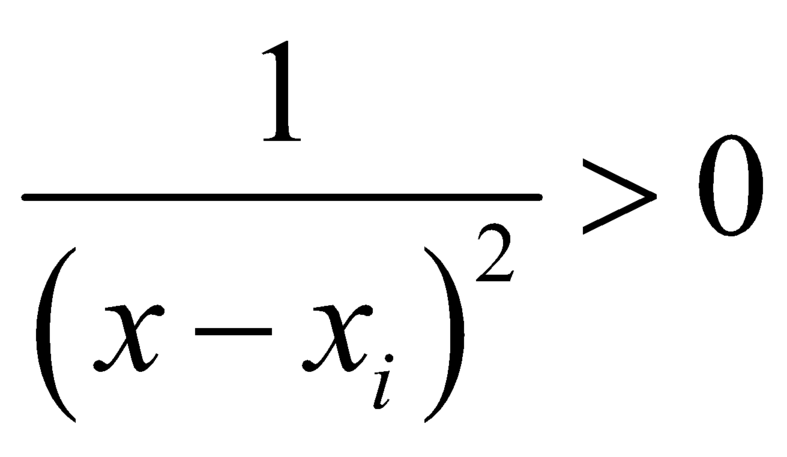 
, 
.
Suy ra 
.
Vậy phương trình 
vô nghiệm hay phương trình 
vô nghiệm.
Do đó, số giao điểm của đồ thị hàm số và trục hoành là 0
Đáp án A
+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.
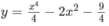
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
Số giao điểm của đồ thị hàm số với trục Ox là hai điểm.
Chọn B