Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(g\left(x\right)=x^4-4x^3+4x^2+a\)
\(g'\left(x\right)=4x^3-12x^2+8x=0\Leftrightarrow4x\left(x^2-3x+2\right)\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)
\(f\left(0\right)=f\left(2\right)=\left|a\right|\) ; \(f\left(1\right)=\left|a+1\right|\)
TH1: \(\left\{{}\begin{matrix}M=\left|a\right|\\m=\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a\right|\ge\left|a+1\right|\\\left|a\right|\le2\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{2}{3}\le a\le-\dfrac{1}{2}\\a\le-2\end{matrix}\right.\) \(\Rightarrow a=\left\{-3;-2\right\}\)
TH2: \(\left\{{}\begin{matrix}M=\left|a+1\right|\\m=\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a+1\right|\ge\left|a\right|\\\left|a+1\right|\le2\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-\dfrac{1}{2}\le a\le-\dfrac{1}{3}\\a\ge1\end{matrix}\right.\) \(\Rightarrow a=\left\{1;2;3\right\}\)
Đáp án: D.
Ta có f(x) = x 3 + 3 x 2 - 9x - 7 ⇒ f'(x) = 3 x 2 + 6x - 9 = 0
⇔ 
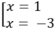
f(-4) = 13, f(-3) = 30, f(1) = -12, f(3) = 20
Vậy min f(x) = -12.
Đáp án: D.
Ta có f(x) = x 3 + 3 x 2 - 9x - 7 ⇒ f'(x) = 3 x 2 + 6x - 9 = 0
⇔ 
f(-4) = 13, f(-3) = 30, f(1) = -12, f(3) = 20
Vậy min f(x) = -12.
Đáp án: A.
Ta có y(0) = -5, y(3) = -2, tọa độ đỉnh: x = -b/2a = 2
⇒ y(2) = -4 + 8 - 5 = -1; max y = max(-5; -2; -1) = -1.
Cách khác: Vì a = -1 nên parabol y = -x2 + 4x - 5 đạt cực đại tại đỉnh (2; -1). Vì vậy GTLN của hàm số trên đoạn [0;3] là y(2) = -1
Đáp án: A.
Ta có y(0) = -5, y(3) = -2, tọa độ đỉnh: x = -b/2a = 2
⇒ y(2) = -4 + 8 - 5 = -1; max y = max(-5; -2; -1) = -1.
Cách khác: Vì a = -1 nên parabol y = - x 2 + 4x - 5 đạt cực đạt tại đỉnh (2; -1). Vì vậy giá trị lớn nhất của hàm số trên đoạn [0;3] là y(2) = -1.
Chọn B
Vì y = a x 3 + c x + d , a ≠ 0 là hàm số bậc ba và có m i n x ∈ - ∞ ; 0 f ( x ) = f ( - 2 ) nên a < 0 và y' = 0 có hai nghiệm phân biệt.
Ta có 
có hai nghiệm phân biệt
⇔
ac < 0
Vậy với a < 0, c > 0 thì y' = 0 có hai nghiệm đối nhau 
Từ đó suy ra
⇔
c = -12a
Ta có bảng biến thiên
Ta suy ra 
