Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Tập xác định: D = ℝ \ 1 2 ⇒ Hàm số y = m x + 1 2 x − 1 liên tục và đơn điệu trên 1 ; 3
⇒ a . b = y 1 . y 3 = m + 1 1 . 3 m + 1 5 = 1 5
⇔ m + 1 3 m + 1 = 1 ⇔ 3 m 2 + 4 m = 0 ⇔ m = 0 m = − 4 3
Vậy có 2 giá trị m thỏa mãn.
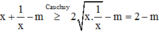



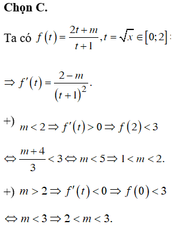


Đáp án D
Tính y’ và tìm nghiệm của y ' = 0 .
- Biện luận các trường hợp điểm x=3 nằm trong, nằm ngoài khoảng 2 nghiệm để suy ra kết luận.
Cách giải:
TXĐ: D = R
y ' = 3 x 2 − 6 m x
Ta có: y ' = 0 ⇔ x = 0 → y = 6 x = 2 m → y = − 4 m 3 + 6
Xét TH1: m=0 . Hàm số đồng biến trên 0 ; 3 . ⇒ M i n 0 ; 3 y = y 0 = 6 → loại.
Xét TH2: m ≥ 3 2 ⇒ 2 m > 3 > 0 . Khi đó, hàm số nghịch biến trên 0 ; 3 ⊂ 0 ; 2 m
⇒ M i n 0 ; 3 y = y 3 = 33 − 27 m = 2 → m = 31 27 < 3 2 (loại)
Xét TH3: 3 2 > m > 0 ⇒ 3 > 2 m > 0 thì đồ thị hàm số có điểm cực đại là 0 ; 6 và điểm cực tiểu là 2 m , − 4 m 3 + 6 .
Khi đó , GTNN trên 0 ; 3 là y 2 m = − 4 m 3 + 6
⇒ − 4 m 3 + 6 = 2 ⇔ m 3 = 1 ⇔ m = 1 (thỏa mãn)
Xét TH4: m < 0 → 0 ; 6 là điểm cực tiểu và trên 0 ; 3 hàm số đồng biến.
⇒ y min = 6 → loại.
Vậy m=1 là giá trị cần tìm.
Đáp án D.
Chú ý khi giải:
HS cần phải xét tất cả các trường hợp và chú ý loại nghiệm. nhiều em sai lầm kết luận m = 31 27 mà không chú ý điều kiện của trường hợp đó là m ≥ 3 2