Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương trình tiếp tuyến của (C) tại M k x k ; y k là y = y k = y ' x k x - x k
⇔ y = y ' x k x - x k + y k = 3 x k 2 - 2018 x - x k + x k 3 - 2018 x k ( d )
Phương trình hoành độ giao điểm của (C) và tiếp tuyến (d) là
x 3 - 2018 x = 3 x k 2 - 2018 x - x k + x k 3 - 2018 x k ⇔ x - x k x 2 + x k x - 2 x k 2 = 0 ⇔ [ x = x k x = - 2 x k Do đó x k + 1 = - 2 x k suy ra x 1 = 1 ; x 2 = - 2 ; x 3 = 4 ; . . . ; x n = ( - 2 ) n - 1 ( cấp số nhân với q = -2)
Vậy 2018 x n + y n + 2 2019 = 0 ⇔ x n 3 = - 2 2019 ⇔ - 2 3 n - 3 = - 2 2019 ⇒ n = 674

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

Chọn đáp án B
Ta có y ' = 3 x 2 - 11 . Giả sử M m ; m 3 - 11 m thì tiếp tuyến ∆ của (C) tại điểm M có hệ số góc là k = y ' m = 3 m 2 - 11
Phương trình ∆ : y = 3 m 2 - 11 x - 2 m .
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng ∆ là:
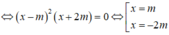
Suy ra hoành độ các điểm Mn lập thành một cấp số nhân (xn) có số hạng đầu x 1 = - 2 và công bội q = -2.
Ta có x n = x 1 . q n - 1 = - 2 n
![]() .
.
Để 11 x n + y n + 2 2019 = 0
⇔ 3 n = 2019 ⇔ n = 673


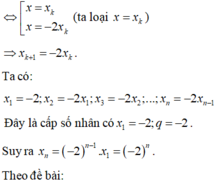

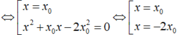
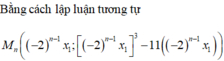

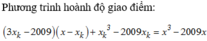
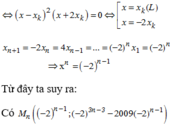
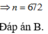

Chọn đáp án C.