Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ Đồ thị hàm số đã cho có tiệm cận đứng là x= -2 và tiệm cận ngang là y= 1.
Giao điểm hai đường tiệm cận là I ( -2; 1) .
Ta có:
A ( a ; 1 - 3 a + 2 ) ∈ ( C ) , B ( b ; 1 - 3 b + 2 ) ∈ ( C ) . I A → = ( a + 2 ; - 3 a + 2 ) , I B → = ( b + 2 ; - 3 b + 2 ) .
Đặt a1== a+ 2 ; b1= b+ 2( a1≠ 0 ; b1≠0 ; a1 ≠ b1
Tam giác ABI đều khi và chỉ khi
Ta có (1)
+ Trường hợp a1= b1 loại
+ Trường hợp a1= - b1 ; a1b1 = -3 (loại vì không thỏa (2) .
+ Trường hợp a1 b1 =3 thay vào ( 2) ta được
3 + 9 3 a 1 2 + 9 a 1 2 = 1 2 ⇔ a 1 2 + 9 a 1 2 = 12 .
Vậy AB=IA= a 1 2 + 9 a 1 2 = 2 3 .
Chọn B.
Ta có đạo hàm y’ = 3x2- 6( m+ 1) x+ 12m.
Hàm số có hai cực trị khi và chỉ khi y’ = 0 có hai nghiệm phân biệt
Hay (m-1) 2> 0 suy ra m≠1 ( *)
Khi đó hai điểm cực trị là A( 2; 9m) : B( 2m; -4m3+ 12m2-3m+ 4).
Tam giác ABC nhận O làm trọng tâm
⇔ 2 + 2 m - 1 = 0 - 4 m 3 + 12 m 2 + 6 m + 4 - 9 2 = 0 ⇔ m = - 1 2 t h ỏ a ( * ) .
Chọn A.
a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)
Phương trình hoành độ giao điểm của (C) và đường thẳng d:
2 x + 1 x - 1 = x + m ( x ≠ 1 ) ⇔ x 2 + ( m - 3 ) x - m - 1 = 0 ( 1 )
Khi đó cắt (C) tại hai điểm phân biệt A: B khi và chi khi phương trình (1) có hai nghiệm phân biệt khác -1
⇔ ( m - 3 ) 2 + 4 ( m + 1 ) > 0 1 2 + ( m - 3 ) - m - 1 ≠ 0 ⇔ m 2 - 2 m + 13 > 0 - 1 ≠ 0 luôn đúng
Gọi A( x1 ; x1+m) ; B( x2 ; x2+m) trong đó x1 ; x2 là nghiệm của (1) , theo Viet ta có
x 1 + x 2 = 3 - m x 1 x 2 = - m - 1
Gọi I ( x 1 + x 2 2 ; ( x 1 + x 2 + 2 m 2 ) là trung điểm của AB, suy ra I ( 3 - m 2 ; 3 + m 2 ) , nên
C I → ( - 2 - 3 - m 2 ; 5 - 3 + m 2 )
⇒ C I = 1 2 ( m - 7 ) 2 + ( 7 - m ) 2 .
Mặt khác A B → = ( x 2 - x 1 ; x 2 - x 1 )
⇒ A B = 2 ( x 2 - x 1 ) 2 = 2 ( m 2 - 2 m + 13 ) 2
Vậy tam giác ABC đều khi và chỉ khi
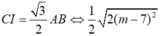
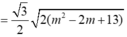
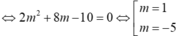
Đáp án A
Gọi 
với 
Do A, B đối xứng nhau qua điểm M(3;3) nên M là trung điểm của AB.
Tính được: 
Chọn D
Phương trình hoành độ giao điểm :
Theo yêu cầu bài toán : 
phải có hai nghiệm phân biệt khác 
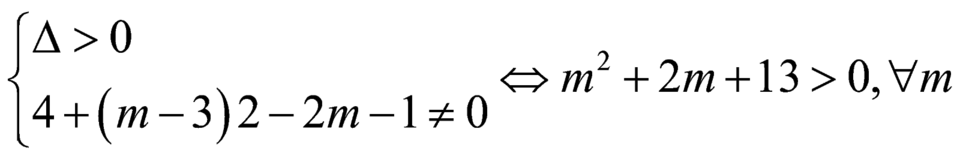
Gọi 
,
suy ra 
là trọng tâm của tam giác 
:
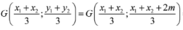
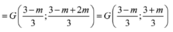
Theo yêu cầu bài toán :
.
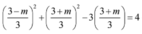
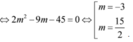Đường tròn (S) tâm \(I\left(-1;-3\right)\) bán kính \(R=3\)
Thế tọa độ A vào pt (S) thỏa mãn nên A nằm trên đường tròn
Ta cần tìm B, C sao cho chi vi ABC lớn nhất
Đặt \(\left(AB;AC;BC\right)=\left(c;b;a\right)\Rightarrow\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}=2R\)
\(\Rightarrow a+b+c=2R\left(sinA+sinB+sinC\right)\)
Mặt khác ta có BĐT quen thuộc \(sinA+sinB+sinC\le\dfrac{3\sqrt{3}}{2}\)
Dấu "=" xảy ra khi tam giác ABC đều
\(\Rightarrow a=b=c=2R.sin60^0=3\sqrt{3}\)
Khi đó I đồng thời là trọng tâm kiêm trực tâm \(\Rightarrow\left\{{}\begin{matrix}BC\perp AI\\d\left(A;BC\right)=\dfrac{a\sqrt{3}}{2}=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow\) Phương trình BC có dạng \(y=-\dfrac{3}{2}\)
Hay (Cm) có 1 tiếp tuyến là \(y=-\dfrac{3}{2}\) (hệ số góc bằng 0 nên tiếp tuyến này đi qua 2 cực tiểu)
\(\Rightarrow m=-1\)
Chọn đáp án B.
ta có hệ điều kiện:
Vậy A - 1 ; - 1 , B 1 ; 3
→ A B = 2 2 + 4 2 = 2 5