Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Có y ' = 1 x − 1 2 . Hàm số đồng biến trên tứng khoảng ( ta chỉ xét khoảng liên tục, không bị ngắt khoảng).

Đáp án C
Ta có f ' x = 0 ⇔ x = 1 ; 2 ; 3 ⇒ hàm số có 3 điểm cực trị
Lại có g x = f x - m - 2018 ⇒ g ' x = f ' x = 0 ⇒ có 3 nghiệm phân biệt
Suy ra phương trình f x = m + 2018 có nhiều nhất 4 nghiệm
Xét y = f x + 1 ⇒ y ' = f ' x + 1 < 0 ⇔ [ x + 1 ∈ 1 ; 2 x + 1 ∈ 3 ; + ∞ ⇔ [ 0 < x < 1 x > 2
Suy ra hàm số y = f(x + 1) nghịch biến trên khoảng (0;1).

Đáp án D
Tại -1 hàm số không xác định nên không nghịch biến trên ( - ∞ ; 3 )

Chọn C.
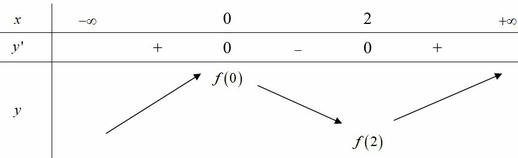
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.

Đáp án B.
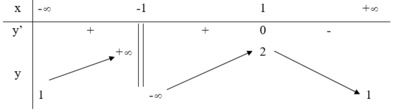
Đồ thị hàm số có 2 tiệm cận, 1 tiệm cận đứng, 1 tiệm cận ngang.
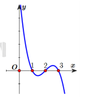
Phương trình f(x) = m có 3 nghiệm thực phân biệt thì m ∈ 1 ; 2 .
Phương án D bị gián đoạn bởi tập xác định.
Phương án C sai vì đồ thị hàm số có dáng điệu tiến đến vô cùng.



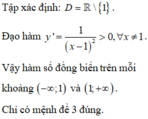


 Xét các khẳng định sau:
Xét các khẳng định sau: 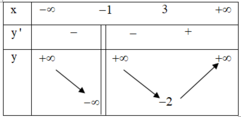


Đáp án D
Phương pháp:
Hàm số dạng y = a x + b c x + d luôn đồng biến hoặc nghịch biến trên từng khoảng xác định của nó.
Cách giải: Tập xác định D = ℝ \ 1
Ta có: y ' = − 1 + 2 x − 1 2 = 1 x − 1 2 > 0 ∀ x ∈ ℝ
Vậy hàm số đồng biến trên các khoảng − ∞ ; 1 và 1 ; + ∞