Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta tính \(y'=\frac{x\left(x-2\right)}{\left(x-1\right)^2}\)
giải pt y'=0
ta có \(x\left(x-2\right)=0\) suy ra x=0 hoặc x=2
bảng bt
x y' y -2 0 1/2 2 0 0 + - -7/3 -1 -3/2
hàm số đạt giá trị lớn nhất =-1 tại x=0, đạt giá trị nhỏ nhất =-7/3 tại x=-2

Đáp án B
Tập xác định: D = ℝ \ 1 2 ⇒ Hàm số y = m x + 1 2 x − 1 liên tục và đơn điệu trên 1 ; 3
⇒ a . b = y 1 . y 3 = m + 1 1 . 3 m + 1 5 = 1 5
⇔ m + 1 3 m + 1 = 1 ⇔ 3 m 2 + 4 m = 0 ⇔ m = 0 m = − 4 3
Vậy có 2 giá trị m thỏa mãn.

ta tính
\(y'=3x^2-6x=3x\left(x-2\right)\)
giải pt y'= 0 ta có \(3x\left(x-2\right)=0\) suy ra x=0 hoặc x=2
x y' -3 0 1 2 0 0 y + -55 -1 -3 - -
nhìn vào bảng bt ta có giái trị lớn nhất của hàm số =3 khi x=0, hàm số đạt giá trị nhỏ nhất =-55 khi x=-3
hàm số đạt giái trị lớn nhất =-1 khi x=0, nhỏ nhất =-55 khi x=-3

Đáp án C.
Xét hàm số y = x 2 - 1 x - 2 trên D, có f ' x = 1 - 2 x x - 2 2 x 2 - 1 ; ∀ x ∈ D .
Trên khoảng - ∞ ; - 1 ; có f ' x > 0 ⇒ f x là hàm số đồng biến trên - ∞ ; - 1
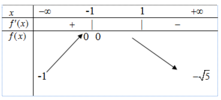
Trên khoảng 1 ; 3 2 , có f ' x < 0 ⇒ f x f(x) là hàm số nghịch biến trên 1 ; 3 2 .
Dựa vào BBT, suy ra M = f 1 = 0 và m = f 3 2 = - 5 . Vậy P = M.m = 0

Đáp án B.
Từ
f x . f ' x = 2 x f 2 x + 1 ⇒ f x . f ' x f 2 x + 1 = 2 x ⇒ ∫ f x . f ' x f 2 x + 1 d x = ∫ 2 x d x
(1)
Đặt
f 2 x + 1 = t ⇒ f 2 x = t 2 − 1 ⇒ 2 f x . f ' x d x = 2 t d t ⇒ f x . f ' x d x = t d t
Suy ra ∫ f x . f ' x f 2 x + 1 x = ∫ t d t t = ∫ d t = t + C 1 = f 2 x + 1 + C 1 và ∫ 2 x d x = x 2 + C 2
Từ (1) ta suy ra f 2 x + 1 + C 1 = x 2 + C 2 . Do f 0 = 0 nên C 2 − C 1 = 1 .
Như vậy
f 2 x + 1 = x 2 + C 2 − C 1 = x 2 + 1 ⇒ f 2 x = x 2 + 1 2 − 1 = x 4 + 2 x 2
⇒ f x = x 4 + 2 x 2 = x x 2 + 2 = x x 2 + 2
(do x ∈ 1 ; 3 ).
Ta có f ' x = x 2 + 2 + x 2 x 2 + 2 = 2 x 2 + 1 x 2 + 2 > 0, ∀ x ∈ ℝ ⇒ Hàm số f x = x x 2 + 2 đồng biến trên R nên f x cũng đồng biến trên 1 ; 3 .
Khi đó M = max 1 ; 3 f x = f 3 = 3 11 và m = min 1 ; 3 f x = f 1 = 3 .
Vậy
P = 2 M − m = 6 11...

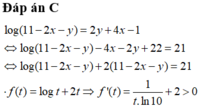
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

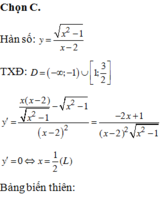
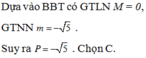

Chọn đáp án C