OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

Mini game 20/11 tri ân thầy cô, nhận thưởng hấp dẫn - Tham gia ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
10 tháng 11 2018

Cho hàm số y =   x - 1 x 2     - 2 x   + m   . Để đồ thị hàm số có 3 tiệm cận thì tất cả giá trị của m là.

A. m=1

B. m<1

C. m>1

D. Không tồn tại
#Mẫu giáo
1
CM
Cao Minh Tâm
10 tháng 11 2018

Đúng(0)
PT
Pham Trong Bach
16 tháng 11 2017
Tìm tất cả giá trị của tham số m để đồ thị hàm số  y = x - m x 2 - ( m + 1 ) x + m có hai tiệm cận A.  m ≠ 1   B.  m ≥ 1   C.  m ≤ 1   D.  m ∈ ℝ ...
Đọc tiếp

Tìm tất cả giá trị của tham số m để đồ thị hàm số  y = x - m x 2 - ( m + 1 ) x + m có hai tiệm cận

A.  m ≠ 1  

B.  m ≥ 1  

C.  m ≤ 1  

D.  m ∈ ℝ

#Mẫu giáo
1
CM
Cao Minh Tâm
16 tháng 11 2017

Đúng(0)
PT
Pham Trong Bach
26 tháng 8 2019
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x − 3 m x − 1  không có tiệm cận đứng A. m = 0 B.  m ≠ 0 C.  m = 0  hoặc  m = 1 3 D.  m = 1 3 ...
Đọc tiếp

Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x − 3 m x − 1  không có tiệm cận đứng

A. m = 0

B.  m ≠ 0

C.  m = 0  hoặc  m = 1 3

D.  m = 1 3

#Mẫu giáo
1
CM
Cao Minh Tâm
26 tháng 8 2019

Đáp án D

Ta có:  A ' C = A B 3 = a 3 ⇒ A B = a ⇐ V = a 3 .

Đúng(0)
PT
Pham Trong Bach
11 tháng 5 2017
Tìm tất cả giá trị thực của tham số m để đồ thị hàm số y = x - 1 2 x 2 - 2 x - m - x - 1 có đúng bốn đường tiệm cận? A.  m ∈ - 5 ; 4 \ - 4 B. m ∈ ( - 5 ; 4 ] C. m ∈ - 5 ; 4 \ - 4 D. m ∈ ( ...
Đọc tiếp

Tìm tất cả giá trị thực của tham số m để đồ thị hàm số y = x - 1 2 x 2 - 2 x - m - x - 1 có đúng bốn đường tiệm cận?

A.  m ∈ - 5 ; 4 \ - 4

B. m ∈ ( - 5 ; 4 ]

C. m ∈ - 5 ; 4 \ - 4

D. m ∈ ( - 5 ; 4 ] \ - 4

#Mẫu giáo
1
CM
Cao Minh Tâm
11 tháng 5 2017

Đáp án D


Đúng(0)
PT
Pham Trong Bach
5 tháng 1 2020
Cho hàm số y = f(x) thỏa mãn l i m x → - ∞ f x   =   - 1  và  l i m x → + ∞ f x   =   m  Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y   =   1 f x + 2  có duy nhất một tiệm cận ngang. A. m = -1 B. m = 2 C.  m ∈ - ...
Đọc tiếp

Cho hàm số y = f(x) thỏa mãn l i m x → - ∞ f x   =   - 1  và  l i m x → + ∞ f x   =   m  Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y   =   1 f x + 2  có duy nhất một tiệm cận ngang.

A. m = -1

B. m = 2

C.  m ∈ - 1 ; - 2

D. m ∈ - 1 ; 2

#Mẫu giáo
1
CM
Cao Minh Tâm
5 tháng 1 2020

Ta có  đồ thị hàm số luôn có TCN y = 1

Do đó để ycbt thỏa mãn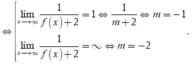  

Chọn C.

Đúng(0)
PT
Pham Trong Bach
25 tháng 11 2018

Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x + 1 m 2 x 2 - m + 1  có đúng 4 đường tiệm cận?

A.  m > 1

B.  m < 1 m ≢ 0

C.  m < 1

D.  m < 0

#Mẫu giáo
1
CM
Cao Minh Tâm
25 tháng 11 2018

Đúng(0)
PT
Pham Trong Bach
9 tháng 6 2019
Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số y = x − 1 + 2017 x 2 − 2 m x + m + 2  đúng 3 đường tiệm cận? A.  2 < m ≤ 3                   B.  2 ≤ m ≤ 3               C.  m < 2                   D.  m > 2  hoặc  m < − 1 ...
Đọc tiếp

Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số y = x − 1 + 2017 x 2 − 2 m x + m + 2  đúng 3 đường tiệm cận?

A.  2 < m ≤ 3                  

B.  2 ≤ m ≤ 3              

C.  m < 2                  

D.  m > 2  hoặc  m < − 1  
#Mẫu giáo
1
CM
Cao Minh Tâm
9 tháng 6 2019

Đáp án A

Ta có: lim x → + ∞ y = 0 ⇒  đồ thị hàm số có 1 tiệm cận ngang là y = 0 .

Để đồ thị hàm số có 3 tiệm cận thì phương trình : g x = x 2 − 2 m x + m + 2 = 0  có 2 nghiệm phân biệt

x 1 > x 2 ⇔ Δ ' = m 2 − m − 2 > 0 x 1 − 1 x 2 − 1 ≥ 0 x 1 − 1 + x 2 − 1 > 0 ⇔ m + 1 m − 2 > 0 x 1 x 2 − x 1 + x 2 + 1 ≥ 0 x 2 + x 2 > 2 ⇔ m + 1 m − 2 > 0 m + 2 − 2 m + 1 > 0 2 m > 2 ⇔ 3 ≥ m > 2.  

Đúng(0)
PT
Pham Trong Bach
15 tháng 3 2019
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = x 2 x 2 − 2 x − m − x − 1  có hai tiệm cận đứng A. m ≥ 4 B. − 5 < m ≤ 4 C. m > − 5 D. − 5 < m ≤ 4 m ≠ − 1 ...
Đọc tiếp

Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = x 2 x 2 − 2 x − m − x − 1  có hai tiệm cận đứng

A. m ≥ 4

B. − 5 < m ≤ 4

C. m > − 5

D. − 5 < m ≤ 4 m ≠ − 1

#Mẫu giáo
1
CM
Cao Minh Tâm
15 tháng 3 2019

Đáp án C

Đúng(0)
PT
Pham Trong Bach
11 tháng 9 2019
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = x 2 x 2 − 2 x − m − x − 1  có hai tiệm cận đứng A.  m ≥ 4 B.  − 5 < m ≤ 4 C. m > − 5 D.  − 5 < m ≤ 4 m ≠ − 1 ...
Đọc tiếp

Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = x 2 x 2 − 2 x − m − x − 1  có hai tiệm cận đứng

A.  m ≥ 4

B.  − 5 < m ≤ 4

C. m > − 5

D.  − 5 < m ≤ 4 m ≠ − 1

#Mẫu giáo
1
CM
Cao Minh Tâm
11 tháng 9 2019

Đáp án C

Ta có  y = x 2 x 2 − 2 x − m + x + 1 x 2 − 4 x − m − 1

Điều kiện đặt ra là mẫu có 2 nghiệm => Δ ' = 5 + m > 0 < = > m > − 5

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP