Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với \(-2\le x\le3\) => \(x+2\ge0\)và \(3-x\ge0\)
Áp dụng BĐT Cosi ta được :
\(y=\left(x+2\right)\left(3-x\right)\le\left[\frac{\left(x+2\right)+\left(3-x\right)}{2}\right]^2=\frac{25}{4}\)
\(\Rightarrow y_{Max}=\frac{25}{4}\) , khi \(x+2=3-x\Leftrightarrow x=\frac{1}{2}\)

Thay x=2 và y=6 vào (d), ta được:
2(m+2)+2m-6=6
=>4m+4+2m-6=6
=>6m-2=6
=>6m=8
=>\(m=\dfrac{4}{3}\)
Khi m=4/3 thì (d): \(y=\left(\dfrac{4}{3}+2\right)x+2\cdot\dfrac{4}{3}-6=\dfrac{10}{3}x-\dfrac{10}{3}\)
Gọi A(x,y) và B(x,y) lần lượt là giao điểm của (d) với trục Ox và Oy
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\dfrac{10}{3}x-\dfrac{10}{3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\dfrac{10}{3}x=\dfrac{10}{3}\end{matrix}\right.\)
=>x=1 và y=0
=>A(1;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\dfrac{10}{3}\cdot0-\dfrac{10}{3}=-\dfrac{10}{3}\end{matrix}\right.\)
=>\(B\left(0;-\dfrac{10}{3}\right)\)
O(0;0); A(1;0); B(0;-10/3)
=>\(OA=\sqrt{\left(1-0\right)^2+\left(0-0\right)^2}=1\)
\(OB=\sqrt{\left(0-0\right)^2+\left(-\dfrac{10}{3}-0\right)^2}=\dfrac{10}{3}\)
\(AB=\sqrt{\left(0-1\right)^2+\left(-\dfrac{10}{3}-0\right)^2}=\dfrac{\sqrt{109}}{3}\)
Vì \(OA^2+OB^2=AB^2\)
nên ΔOAB vuông tại O
Kẻ OH vuông góc AB tại H
=>OH là khoảng cách từ O đến (d)
Xét ΔOAB vuông tại O có OH là đường cao
nên \(OH\cdot AB=OA\cdot OB\)
\(\Leftrightarrow OH\cdot\dfrac{\sqrt{109}}{3}=1\cdot\dfrac{10}{3}\)
=>\(OH=\dfrac{10}{\sqrt{109}}\)
=>\(d\left(O;\left(d\right)\right)=\dfrac{10}{\sqrt{109}}\)
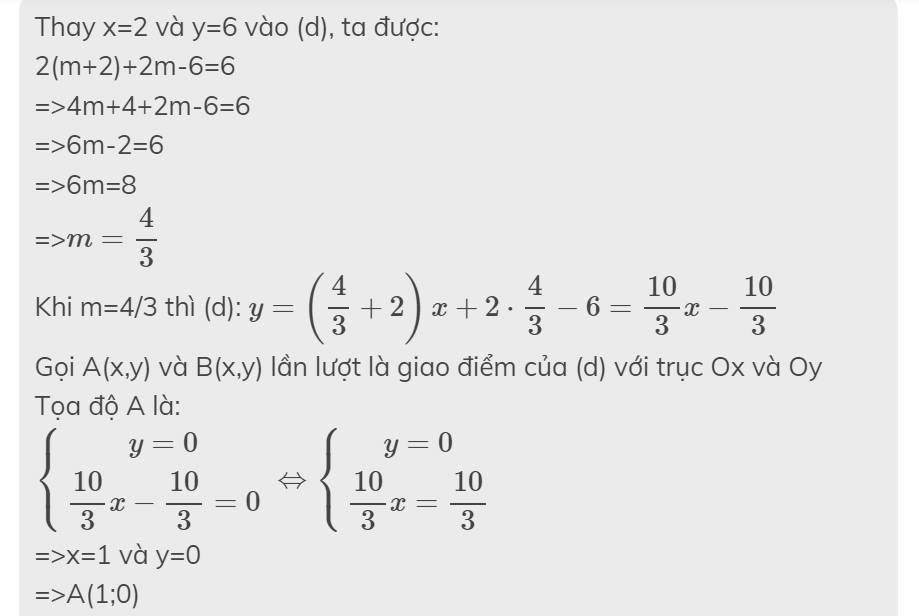

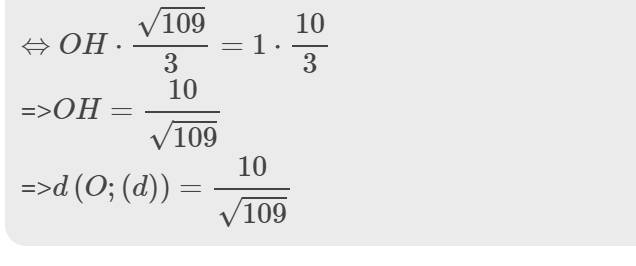
Giải:
y = (m -2)\(x\) + 2
⇒ (m- 2)\(x\) - y + 2 = 0
Gốc tọa độ O(0; 0)
Khoảng cách từ gốc tọa độ O(0; 0) đến đường thẳng (d) là:
d(O;d) = \(\frac{\left|\left(m-2\right)\right..0-1.0+2\left|\right.}{\sqrt{\left(m-2\right)^2+1}}\) = \(\frac{2}{\sqrt{\left(m-2\right)^2+1}}\)
Khoảng cách từ gốc tọa độ O đến đường thẳng (d) là lớn nhất khi A = \(\frac{2}{\sqrt{\left(m-2\right)^2+1}}\) lớn nhất.
Vì 2 > 0; \(\sqrt{\left(m-2\right)^2+1}\) > 0 ∀ m nên
A lớn nhất khi (m - 2)\(^2\) + 1 là nhỏ nhất.
(m - 2)\(^2\) ≥ 0 ∀ m
(m - 2)\(^2\) + 1 ≥ 1 ∀ m
\(\sqrt{\left(m-2\right)^2+1}\) ≥ 1 ∀ m
A = \(\frac{2}{\sqrt{\left(m-2^{}\right)^2+1}}\) ≤ \(\frac21=2\) dấu bằng xảy khi m - 2 = 0
suy ra m = 2
Vậy khoảng cách từ gốc tọa độ đến đồ thị lớn nhất là \(2\) khi m = 2