Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số y = (m+1)x -2m là hàm bậc nhất khi m+1 ≠ 0 ⇔ m ≠ - 1
a) Hàm số nghịch biến trên R khi a < 0 ⇔ m + 1< 0 ⇔ m < - 1
kết hợp với điều kiện. Vậy m < -1
b) Khi m = 1 ta được: y = (1+1)x - 2.1 hay y = 2x - 2
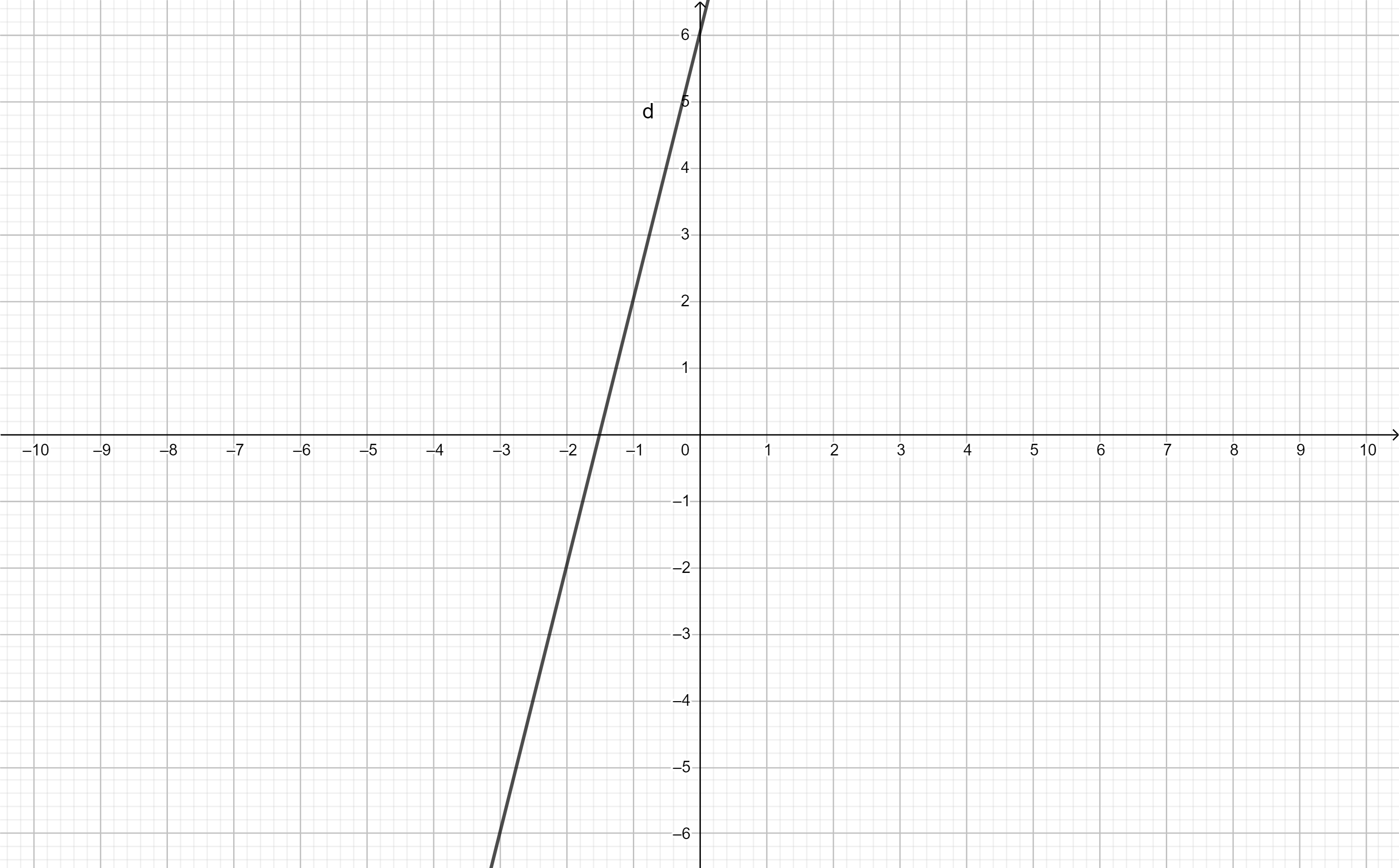
Đồ thị hàm số y = 2x - 2 đi qua hai điểm A(0;-2) và B(1;0)
c) Đồ thị của hai hàm số song song với nhau khi \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+1=3\\-2m\ne6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2\\m\ne-3\end{matrix}\right.\)
kết hợp với điều kiện. Vậy m = 2
Tham Khảo:
Hàm số y = (m+1)x -2m là hàm bậc nhất khi m+1 ≠ 0 ⇔ m ≠ - 1
a) Hàm số nghịch biến trên R khi a < 0 ⇔ m + 1< 0 ⇔ m < - 1
kết hợp với điều kiện. Vậy m < -1
b) Khi m = 1 ta được: y = (1+1)x - 2.1 hay y = 2x - 2
Đồ thị hàm số y = 2x - 2 đi qua hai điểm A(0;-2) và B(1;0)
c) Đồ thị của hai hàm số song song với nhau khi
kết hợp với điều kiện. Vậy m = 2


a,sửa đề y = (m+1)x - 2m (d)
để (d) nghịch biến khi m < -1
b, \(\left\{{}\begin{matrix}m+1=3\\-2m\ne6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2\\m\ne-3\end{matrix}\right.\)<=> m = 2 (ktmđk)
vậy ko có gtri m để (d) // y = 3x + 6

a) Để hàm số là hàm bậc nhất thì 3 - m 0
m 3
b) Để hàm số là nghịch biến thì 3 - m < 0
m > 3
c) Thay tọa độ điểm A(2; -3) vào hàm số, ta được:
(3 - m).2 + 2 = -3
6 - 2m + 2 = -3
8 - 2m = -3
2m = 11
m = 11/2 (nhận)
Vậy m = 11/2 thì đồ thị hàm số đi qua A(2; -3)
(Sửa theo yêu cầu rồi nhé em!)
d) Thay tọa độ B(-1; -5) vào hàm số, ta được:
(2 - m).(-1) + 2 = -5
-2 + m + 2 = -5
m = -5 (nhận)
Vậy m = -5 thì đồ thị hàm số đi qua B(-1; -5)

Để hàm số đã cho đồng biến thì \(m^2-5m-6>0\)\(\Leftrightarrow m^2+m-6m-6>0\)\(\Leftrightarrow m\left(m+1\right)-6\left(m+1\right)>0\)\(\Leftrightarrow\left(m+1\right)\left(m-6\right)>0\)
Trường hợp 1: \(\hept{\begin{cases}m+1>0\\m-6>0\end{cases}}\Leftrightarrow\hept{\begin{cases}m>-1\\m>6\end{cases}}\Rightarrow m>6\)
Trường hợp 2: \(\hept{\begin{cases}m+1< 0\\m-6< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}m< -1\\m< 6\end{cases}}\Rightarrow m< -1\)
Vậy để hàm số đã cho đồng biến thì \(m>6\)hoặc \(m< -1\)
Để hàm số đã cho nghịch biến thì \(m^2-5m-6< 0\)\(\Leftrightarrow\left(m+1\right)\left(m-6\right)< 0\)
Trường hợp 1: \(\hept{\begin{cases}m+1< 0\\m-6>0\end{cases}}\Leftrightarrow\hept{\begin{cases}m< -1\\m>6\end{cases}}\)(loại vì m không thể vừa nhỏ hơn -1 lại vừa lớn hơn 6)
Trường hợp 2: \(\hept{\begin{cases}m+1>0\\m-6< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}m>-1\\m< 6\end{cases}}\Rightarrow-1< m< 6\)
Vậy để hàm số đã cho nghịch biến thì \(-1< m< 6\)

) Điều kiện để hàm số xác định là m≥0m≥0; x∈Rx∈R
Để hàm số đã cho là hàm bậc nhất thì m√+3√m√+5√≠0m+3m+5≠0
Vì m−−√+3–√≥0+3–√>0m+3≥0+3>0 với mọi m≥0m≥0 nên m−−√+3–√≠0,∀m≥0m+3≠0,∀m≥0
⇒m√+3√m√+5√≠0⇒m+3m+5≠0 với mọi m≥0m≥0
Vậy hàm số là hàm bậc nhất với mọi m≥0m≥0
b)
Để hàm đã cho nghịch biến thì m√+3√m√+5√<0m+3m+5<0
Điều này hoàn toàn vô lý do {m−−√+3–√≥3–√>0m−−√+5–√≥5–√>0{m+3≥3>0m+5≥5>0
Vậy không tồn tại mm để hàm số đã cho nghịch biến trên R
Giải thích các bước giải:

a. \(\left\{{}\begin{matrix}DB:m+4>0\Leftrightarrow m>-4\\NB:m+4< 0\Leftrightarrow m< -4\end{matrix}\right.\)
\(a,\) Đồng biến \(\Leftrightarrow m+4>0\Leftrightarrow m>-4\)
Nghịch biến \(m+4< 0\Leftrightarrow m< -4\)
\(b,A\left(-1;2\right)\in\left(d\right)\Leftrightarrow-m-4-m+6=2\Leftrightarrow m=0\)
\(\Leftrightarrow y=4x+6\)

Lời giải:
a. Để hàm đồng biến thì $m-1>0\Leftrightarrow m>1$
Để hàm nghịch biến thì $m-1<0\Leftrightarrow m< 1$
b. Để đths đi qua điểm $A(-1;1)$ thì:
$y_A=(m-1)x_A+m$
$\Leftrightarrow 1=(m-1)(-1)+m=1-m+m$
$\Leftrightarrow 1=1$ (luôn đúng)
Vậy đths luôn đi qua điểm A với mọi $m$
c.
$x-2y=1\Rightarrow y=\frac{1}{2}x-\frac{1}{2}$
Để đths đã cho song song với đths $y=\frac{1}{2}x-\frac{1}{2}$ thì:
\(\left\{\begin{matrix} m-1=\frac{1}{2}\\ m\neq \frac{-1}{2}\end{matrix}\right.\Leftrightarrow m=\frac{3}{2}\)
d,
ĐTHS cắt trục hoành tại điểm có hoành độ $\frac{2-\sqrt{3}}{2}$, tức là ĐTHS đi qua điểm $(\frac{2-\sqrt{3}}{2}; 0)$
$\Rightarrow 0=(m-1).\frac{2-\sqrt{3}}{2}+m$
$\Leftrightarrow m=\frac{2-\sqrt{3}}{4-\sqrt{3}}$
Hàm số y = m 2 − 3 x + m + 1 là hàm số nghịch biến khi
m 2 − 3 < 0 ⇔ m 2 < 3 ⇔ m < 6
Đáp án cần chọn là: C