Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có f ' x = 0 ⇔ x = 1 ; 2 ; 3 ⇒ hàm số có 3 điểm cực trị
Lại có g x = f x - m - 2018 ⇒ g ' x = f ' x = 0 ⇒ có 3 nghiệm phân biệt
Suy ra phương trình f x = m + 2018 có nhiều nhất 4 nghiệm
Xét y = f x + 1 ⇒ y ' = f ' x + 1 < 0 ⇔ [ x + 1 ∈ 1 ; 2 x + 1 ∈ 3 ; + ∞ ⇔ [ 0 < x < 1 x > 2
Suy ra hàm số y = f(x + 1) nghịch biến trên khoảng (0;1).

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Đáp án B
Phương pháp: Từ đồ thị hàm số y = f’(x) lập BBT của đồ thị hàm số y = f(x) và kết luận.
Cách giải: Ta có 
BBT:
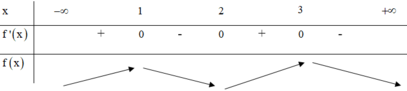
Từ BBT ta thấy (I) đúng, (II) sai.
Với ![]() => Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=> Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=>(III) đúng.
Vậy có hai khẳng định đúng

Từ \(f\left(x\right)+f\left(\frac{1}{x}\right)=x^2\); lần lượt thay \(x=2\) và \(x=\frac{1}{2}\) vào, ta có:
\(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\) và \(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\Leftrightarrow3f\left(2\right)+f\left(\frac{1}{2}\right)=\frac{1}{4}\)
Giải hệ phương trình với 2 ẩn \(f\left(2\right)\) và \(f\left(\frac{1}{2}\right)\)
Tìm được \(f\left(2\right)=\frac{-13}{32}\)
Ta có \(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\) (1)
Thay \(x\rightarrow\frac{1}{x}\) được \(f\left(\frac{1}{x}\right)+3f\left(x\right)=\frac{1}{x^2}\)
\(\Leftrightarrow3f\left(\frac{1}{x}\right)+9f\left(x\right)=\frac{3}{x^2}\) (2)
Lấy (2) trừ (1) theo vế : \(8f\left(x\right)=\frac{3}{x^2}-x^2\)
\(\Leftrightarrow f\left(x\right)=\frac{1}{8}\left(\frac{3}{x^2}-x^2\right)\)
Vậy f(2) = -13/32

Đáp án D
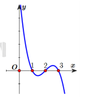
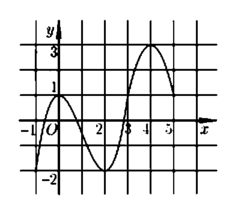
Dựa vào hình vẽ, ta thấy rằng
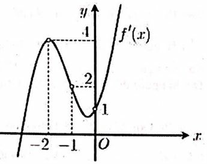
+ Đồ thị hàm số f '(x) cắt Ox tại 3 điểm phân biệt x 1 - 1 ; 0 , x 2 0 ; 1 , x 3 2 ; 3
Và f '(x) đổi dấu từ - → + khi đi qua x 1 , x 3 ⇒ Hàm số có 2 điểm cực tiểu, 1 điểm cực đại
+ Hàm số y = f(x) nghịch biến trên khoảng - 1 ; x 1 đồng biến trên x 1 ; x 2 (1) sai
+ Hàm số y = f(x) nghịch biến trên khoảng x 2 ; x 3 (chứa khoảng (1;2)), đồng biến trên khoảng x 3 ; 5 (chứa khoảng (3;5)) ⇒ 2 ; 3 đúng
Vậy mệnh đề 2,3 đúng và 1, 4 sai.

Chọn C.
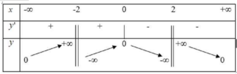
Phương pháp: Dựa vào bảng biến thiên để xác định tiệm cận, cực trị, giá trị lớn nhất, giá trị nhỏ nhất.
Cách giải: Dựa vào bảng biến thiên dễ thấy đồ thị hàm số có tiệm cận ngang y = 0 và hai tiệm cận đứng x = 2, x = -2. Vậy (I) sai và (IV) đúng.



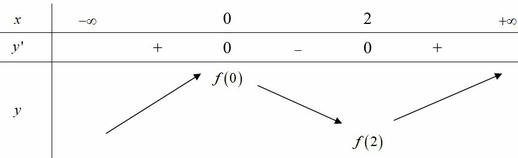



 Xét các khẳng định sau:
Xét các khẳng định sau: 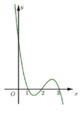


Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)
Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.